
分析 斜率是直线y=-$\sqrt{3}$x+1的斜率的-$\frac{1}{3}$,即$\frac{\sqrt{3}}{3}$,
(1)利用点斜式,可得直线方程;
(2)利用截距式,可得直线方程.
解答 解:斜率是直线y=-$\sqrt{3}$x+1的斜率的-$\frac{1}{3}$,即$\frac{\sqrt{3}}{3}$,
(1)经过点($\sqrt{3}$,-1),方程为y+1=$\frac{\sqrt{3}}{3}$(x-$\sqrt{3}$),即x-$\sqrt{3}$y-2$\sqrt{3}$=0;
(2)在y轴上的截距为-5,方程为y=$\frac{\sqrt{3}}{3}$x-5.
点评 本题考查直线方程,考查学生的计算能力,比较基础.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
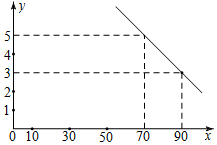 近几年,由于环境的污染,雾霾越来越严重,某环保公司销售一种PM2.5颗粒物防护口罩深受市民欢迎.已知这种口罩的进价为40元,经销过程中测出年销售量y(万件)与销售单价x(元)存在如图所示的一次函数关系,每年销售这种口罩的总开支z(万元)(不含进价)与年销量y(万件)存在函数关系z=10y+42.5.
近几年,由于环境的污染,雾霾越来越严重,某环保公司销售一种PM2.5颗粒物防护口罩深受市民欢迎.已知这种口罩的进价为40元,经销过程中测出年销售量y(万件)与销售单价x(元)存在如图所示的一次函数关系,每年销售这种口罩的总开支z(万元)(不含进价)与年销量y(万件)存在函数关系z=10y+42.5.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ③④ | B. | ②③ | C. | ①④ | D. | ①② |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com