
设函数![]() ,
,![]() ,F(x)=xf(x).
,F(x)=xf(x).
(Ⅰ)若函数y=f(x)在x=2处有极值,求实数m的值;
(Ⅱ)试讨论方程![]() 的实数解的个数;
的实数解的个数;
(Ⅲ)记函数y=G(x)的导称函数![]() 在区间(a,b)上的导函数为
在区间(a,b)上的导函数为![]() ,若在(a,b)上
,若在(a,b)上![]() >0恒成立,则称函数G(x)(a,b)上为“凹函数”.若存在实数m∈[-2,2],使得函数F(x)在(a,b)上为“凹函数”,求b-a最大值.
>0恒成立,则称函数G(x)(a,b)上为“凹函数”.若存在实数m∈[-2,2],使得函数F(x)在(a,b)上为“凹函数”,求b-a最大值.
|
本题主要考查函数、导数知识及其应用,考查运算求解能力及抽象概括能力,考查函数与方程、分类与整合、数形结合、化归与转化等思想方法. (Ⅱ) 即 令 ∴ 由图知,
当 当 当 当 当 综上所述, (Ⅲ) 则 m∈[-2,2] |


科目:高中数学 来源:2011年普通高等学校招生全国统一考试文科数学试题新课标卷 题型:013
设函数,则f(x)=sin(2x+![]() )+cos(2x+
)+cos(2x+![]() )
)
y=f(x)在(0,![]() )单调递增,其图像关于直线x=
)单调递增,其图像关于直线x=![]() 对称
对称
y=f(x)在(0,![]() )单调递增,其图像关于直线x=
)单调递增,其图像关于直线x=![]() 对称
对称
y=f(x)在(0,![]() )单调递减,其图像关于直线x=
)单调递减,其图像关于直线x=![]() 对称
对称
y=f(x)在(0,![]() )单调递减,其图像关于直线x=
)单调递减,其图像关于直线x=![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源:2012年人教A版高中数学必修四1.4三角函数的图像与性质练习卷(二)(解析版) 题型:选择题
设f(x)是定义域为R,最小正周期为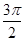 的函数,若f(x)=
的函数,若f(x)=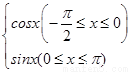 ,则f
,则f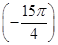
的值等于( )
A.1 B.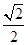
C.0 D.-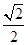 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)当x>a时,求证:f(x)<x;
(2)求证:|f(x1)-f(x2)|<|x1-x2|(x1,x2∈R,x1≠x2);
(3)试举一个定义域为R的函数f(x),满足0<f′(x)<1,且f′(x)不为常数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com