【题目】已知正方形ABCD的边长为1，弧BD是以点A为圆心的圆弧．
（1）在正方形内任取一点M，求事件“|AM|≤1”的概率；
（2）用大豆将正方形均匀铺满，经清点，发现大豆一共28粒，其中有22粒落在圆中阴影部分内，请据此估计圆周率π的近似值（精确到0.01）．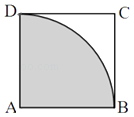 
【答案】
（1）解：如图，在边长为1的正方形ABCD内任取一点M，满足条件的点M落在扇形BAD内（图中阴影部分），由几何概型概率计算公式，有： 
，
故事件“|AM|≤1”发生的概率为 
．
（2）解：正方形内的28粒大豆有22粒落在扇形BAD内，
频率为 
，
用频率估计概率，由（1）知 
，
∴ 
，即π的近似值为3.14．
【解析】（1）根据已知条件，求出满足条件的正方形ABCD的面积，及事件“|AM|≤1”对应平面区域的面积，代入几何概型计算公式，即可求出答案．（2）正方形内的56粒芝麻颗粒中有44粒落在扇形BAD内，频率为 
，用频率估计概率，由（1）知 ，可得圆周率π的近似值．
【考点精析】掌握几何概型是解答本题的根本，需要知道几何概型的特点：1）试验中所有可能出现的结果（基本事件）有无限多个；2）每个基本事件出现的可能性相等．
科目：高中数学 来源： 题型：
【题目】已知函数
（
是常数且
），对于下列命题：
①函数
的最小值是
；
②函数
在
上是单调函数；
③若
在
上恒成立，则
的取值范围是
；
④对任意的
且
，恒有
其中正确命题的序号是__________．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知单调递增的等比数列{an}满足：a2+a3+a4=28，且a3+2是a2 ， a4的等差中项．
（1）求数列{an}的通项公式
（2）若bn=anlog 
an ， Sn=b1+b2+b3+…+bn ， 对任意正整数n，Sn+（n+m）an+1＜0恒成立，试求m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】以（a，1）为圆心，且与两直线x﹣y+1=0及x﹣y﹣3=0同时相切的圆的标准方程为（ ）
A.x2+（y﹣1）2=2
B.（x﹣2）2+（y﹣1）2=2
C.x2+（y﹣1）2=8
D.（x﹣2）2+（y﹣1）2=8
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲乙两台机床同时生产一种零件，10天中，两台机床每天出的次品数分别是
甲 | 0 | 1 | 0 | 2 | 2 | 0 | 3 | 1 | 2 | 4 |
乙 | 2 | 3 | 1 | 1 | 0 | 2 | 1 | 1 | 0 | 1 |
由此判断性能较好的一台是 ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某学校实行自主招生，参加自主招生的学生从8个试题中随机挑选出4个进行作答，至少答对3个才能通过初试．已知甲、乙两人参加初试，在这8个试题中甲能答对6个，乙能答对每个试题的概率为
，且甲、乙两人是否答对每个试题互不影响．
（Ⅰ）求甲通过自主招生初试的概率；
（Ⅱ）试通过概率计算，分析甲、乙两人谁通过自主招生初试的可能性更大；
（Ⅲ）记甲答对试题的个数为
，求
的分布列及数学期望．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列命题中正确的是（ ）
①“若x2+y2≠0，则x，y不全为零”的否命题；
②“正多边形都相似”的逆命题；
③“若m＞0，则x2+x﹣m=0有实根”的逆否命题；
④“若x﹣ 
是有理数，则x是无理数”的逆否命题．
A.①②③④
B.①③④
C.②③④
D.①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
