
【题目】某品牌手机厂商推出新款的旗舰机型,并在某地区跟踪调查得到这款手机上市时间(x个月)和市场占有率(y%)的几组相关对应数据:
x | 1 | 2 | 3 | 4 | 5 |
y | 0.02 | 0.05 | 0.1 | 0.15 | 0.18 |
(1)根据上表中的数据,用最小二乘法求出y关于x的线性回归方程;
(2)根据上述回归方程,分析该款旗舰机型市场占有率的变化趋势,并预测自上市起经过多少个月,该款旗舰机型市场占有率能超过0.5%(精确到月).
附:  ,
, ![]() .
.
【答案】(1) ![]() =0.042x-0.026. (2) 预计上市13个月时,该款旗舰机型市场占有率能超过0.5%.
=0.042x-0.026. (2) 预计上市13个月时,该款旗舰机型市场占有率能超过0.5%.
【解析】试题分析:(1)根据表中数据,计算![]() ,
, ![]() 与
与![]() 写出线性回归方程;
写出线性回归方程;
(2)根据回归方程得出上市时间与市场占有率的关系,列出不等式求出解集即可预测结果.
试题解析:
(1)由题意知![]() =3,
=3,![]() =0.1,
=0.1,![]() iyi=1.92,
iyi=1.92,
![]() =55,
=55,
所以![]() =
= =
=![]() =0.042,
=0.042,
![]() =
=![]() -
-![]()
![]() =0.1-0.042×3=-0.026,
=0.1-0.042×3=-0.026,
所以线性回归方程为![]() =0.042x-0.026.
=0.042x-0.026.
(2)由(1)中的回归方程可知,上市时间与市场占有率正相关,
即上市时间每增加1个月,市场占有率约增加0.042个百分点.
由![]() =0.042x-0.026>0.5,解得x≥13,
=0.042x-0.026>0.5,解得x≥13,
故预计上市13个月时,该款旗舰机型市场占有率能超过0.5%.


科目:高中数学 来源: 题型:
【题目】(本小题满分10分)
某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨,销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元.该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨.那么在一个生产周期内该企业生产甲、乙两种产品各多少吨可获得最大利润,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中的“两鼠穿墙题”是我国数学的古典名题:“今有垣厚若干尺,两鼠对穿,大鼠日一尺,小鼠也日一尺,大鼠日自倍,小鼠日自半,问何日相逢,各穿几何?”题意是:“有两只老鼠从墙的两边打洞穿墙,大老鼠第一天进一尺,以后每天加倍;小老鼠第一天也进一尺,以后每天减半.”如果墙足够厚,![]() 为前
为前![]() 天两只老鼠打洞之和,则
天两只老鼠打洞之和,则![]() _________________尺.
_________________尺.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,且椭圆上任意一点到左焦点的最大距离为
,且椭圆上任意一点到左焦点的最大距离为![]() ,最小距离为
,最小距离为![]() .
.
(1)求椭圆的方程;
(2)过点![]() 的动直线
的动直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,试问:在坐标平面上是否存在一个定点
两点,试问:在坐标平面上是否存在一个定点![]() ,使得以线段
,使得以线段![]() 为直径的圆恒过点
为直径的圆恒过点![]() ?若存在,求出点
?若存在,求出点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地区某种农产品的年产量![]() (单位:吨)对价格
(单位:吨)对价格![]() (单位:千元/吨)和利润
(单位:千元/吨)和利润![]() 的影响,对近五年该农产品的年产量和价格统计如表:
的影响,对近五年该农产品的年产量和价格统计如表:
| 1 | 2 | 3 | 4 | 5 |
| 7.0 | 6.5 | 5.5 | 3.8 | 2.2 |
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)若每吨该农产品的成本为2千元,假设该农产品可全部卖出,预测当年产量为多少时,年利润![]() 取到最大值?(保留两位小数)
取到最大值?(保留两位小数)
参考公式: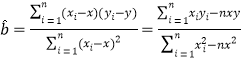 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且 ![]() a=2csinA
a=2csinA
(1)确定角C的大小;
(2)若c= ![]() ,且△ABC的面积为
,且△ABC的面积为 ![]() ,求a+b的值.
,求a+b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设矩形ABCD(AB>AD)的周长为24,把△ABC沿AC向△ADC折叠,AB折过去后交DC于点P,设AB=x,求△ADP的最大面积及相应x的值. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com