
【题目】椭圆![]() 与
与![]() 的中心在原点,焦点分别在
的中心在原点,焦点分别在![]() 轴与
轴与![]() 轴上,它们有相同的离心率
轴上,它们有相同的离心率![]() ,并且
,并且![]() 的短轴为
的短轴为![]() 的长轴,
的长轴,![]() 与
与![]() 的四个焦点构成的四边形面积是
的四个焦点构成的四边形面积是![]() .
.
(1)求椭圆![]() 与
与![]() 的方程;
的方程;
(2)设![]() 是椭圆
是椭圆![]() 上非顶点的动点,
上非顶点的动点,![]() 与椭圆
与椭圆![]() 长轴两个顶点
长轴两个顶点![]() ,
,![]() 的连线
的连线![]() ,
,![]() 分别与椭圆
分别与椭圆![]() 交于
交于![]() ,
,![]() 点.
点.
(i)求证:直线![]() ,
,![]() 斜率之积为常数;
斜率之积为常数;
(ii)直线![]() 与直线
与直线![]() 的斜率之积是否为常数?若是,求出该值;若不是,说明理由.
的斜率之积是否为常数?若是,求出该值;若不是,说明理由.

【答案】(1)![]() ,
,![]() .(2)(i) 见解析(ii)
.(2)(i) 见解析(ii)![]() .
.
【解析】试题分析:(1)椭圆离心率![]() ,又
,又![]() ,所以
,所以![]() ,设
,设![]() ,则根据题中条件可设
,则根据题中条件可设![]() ,于是根据椭圆的对称性可知,四个焦点构成的四边形为菱形,面积
,于是根据椭圆的对称性可知,四个焦点构成的四边形为菱形,面积![]() ,解得
,解得![]() ,可以得到椭圆
,可以得到椭圆![]() ,
,![]() ;(2)(i)本问考查圆锥曲线中的定点、定值问题,分析题意,设
;(2)(i)本问考查圆锥曲线中的定点、定值问题,分析题意,设![]() ,而
,而![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,于是
,于是![]() ,又因为
,又因为![]() ,代入上式易求
,代入上式易求![]() ;(ii)根据(i)问,可先证明
;(ii)根据(i)问,可先证明![]() 为定值,再证明
为定值,再证明![]() 为定值,于是可以得到
为定值,于是可以得到![]() 为定值,由于
为定值,由于![]() ,
,![]() ,所以可以得
,所以可以得![]() 为定值.
为定值.
试题解析:(1)依题意![]() ,设
,设![]() ,
,![]() ,由对称性,四个焦点构成的四边形为菱形,且面积
,由对称性,四个焦点构成的四边形为菱形,且面积![]() ,解得:
,解得:![]() .
.
所以椭圆![]() ,
,![]() .
.
(2)(i)设![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() .
.
所以:![]() .
.
直线![]() ,
,![]() 斜率之积为常数
斜率之积为常数![]() .
.
(ii)设![]() ,则
,则![]() .
.
![]() ,
,![]() ,
,
所以:![]() ,同理:
,同理:![]() ,
,
所以:![]() ,由
,由![]() ,
,![]() ,结合(i)有
,结合(i)有
![]() .
.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:
【题目】在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用,现有6名男志愿者A1,A2,A3,A4,A5,A6和4名女志愿者B1,B2,B3,B4,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示.
(I)求接受甲种心理暗示的志愿者中包含A1但不包含![]() 的频率。
的频率。
(II)用X表示接受乙种心理暗示的女志愿者人数,求X的分布列与数学期望EX.
查看答案和解析>>
科目:高中数学 来源: 题型:
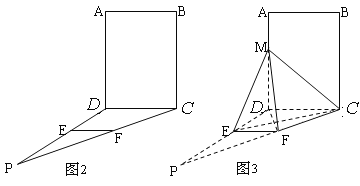
【题目】如图2,四边形![]() 为矩形,
为矩形, ![]() ⊥平面
⊥平面![]() ,
, ![]() ,作如图3折叠,折痕
,作如图3折叠,折痕![]()
![]()
![]() ,其中点
,其中点![]() 分别在线段
分别在线段![]() 上,沿
上,沿![]() 折叠后点
折叠后点![]() 叠在线段
叠在线段![]() 上的点记为
上的点记为![]() ,并且
,并且![]() ⊥
⊥![]() .(1)证明:
.(1)证明: ![]() ⊥平面
⊥平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经济学中,函数f(x)的边际函数M(x)定义为M(x)=f(x+1)﹣f(x),利润函数p(x)边际利润函数定义为M1(x)=p(x+1)﹣p(x),某公司最多生产 100 台报系统装置,生产x台的收入函数为R(x)=3000x﹣20x2(单位:元),其成本函数为C(x)=500x+4000x(单位:元),利润是收入与成本之差.
(1)求利润函数p(x)及边际利润函数M1(x);
(2)利润函数p(x)与边际利润函数M1(x)是否具有相等的最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]()
![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 任作一条直线与椭圆
任作一条直线与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,试问在
两点,试问在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得直线
,使得直线![]() 与直线
与直线![]() 关于
关于![]() 轴对称?若存在,求出点
轴对称?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,且当x>0时,f(x)=( ![]() )x .
)x .
(1)求函数f(x)的解析式;
(2)在所给坐标系中画出函数f(x)的图象,并根据图象写出函数f(x)的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数y=f(x)在区间上[0,1]的图象是连续不断的一条曲线,且恒有0≤f(x)≤1,可以用随机模拟方法近似计算出曲线y=f(x)及直线x=0,x﹣1=0,y=0所围成部分的面积S,先产生两组(每组N个)区间[0,1]上的均匀随机数X1 , X2 , X3 , XN和y1 , y2 , y3 , yN , 由此得到N个点(xi , yi)(i=1,2,3N,再数出其中满足yi≤f(xi)(i=1,2,3,N)的点数N1 , 那么由随机方法可以得到S的近似值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学举行了一次“环保只知识竞赛”,全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为![]() 分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表(如图所示),解决下列问题.
分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表(如图所示),解决下列问题.

(1)求出![]() 的值;
的值;
(2)在选取的样本中,从竞赛成绩是![]() 分以上(含
分以上(含![]() 分)的同学中随机抽取
分)的同学中随机抽取![]() 名同学到广场参加环保只是的志愿宣传活动.
名同学到广场参加环保只是的志愿宣传活动.
1)求所抽取的![]() 名同学中至少有
名同学中至少有![]() 名同学来自第
名同学来自第![]() 组的概率;
组的概率;
2)求所抽取的![]() 名同学来自同一组的概率.
名同学来自同一组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com