
【题目】第十二届全国人民代表大会第五次会议和政协第十二届全国委员会第五次会议(简称两会)分别于2017年3月5日和3月3日在北京开幕,某高校学生会为了解该校学生对全国两会的关注情况,随机调查了该校200名学生,并将这200名学生分为对两会“比较关注”与“不太关注”两类,已知这200名学生中男生比女生多20人,对两会“比较关注”的学生中男生人数比女生人数之比为![]() ,对两会“不太关注”的学生中男生比女生少5人.
,对两会“不太关注”的学生中男生比女生少5人.
(Ⅰ)根据题意建立的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为男生与女生对两会的关注有差异?
的把握认为男生与女生对两会的关注有差异?
(Ⅱ)该校学生会从对两会“比较关注”的学生中根据性别进行分层抽样,从中抽取7人,再从这7人中随机选出2人参与两会宣传活动,求这2人全是男生的概率.
附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
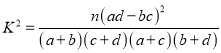 ,
, ![]() .
.
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为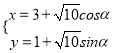 (
(![]() 为参数),以直角坐标系原点
为参数),以直角坐标系原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(1)求曲线![]() 的极坐标方程,并说明其表示什么轨迹;
的极坐标方程,并说明其表示什么轨迹;
(2)若直线的极坐标方程为![]() ,求直线被曲线
,求直线被曲线![]() 截得的弦长.
截得的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于无穷数列![]() 和函数
和函数![]() ,若
,若![]() ,则称
,则称![]() 是数列
是数列![]() 的母函数.
的母函数.
(Ⅰ)定义在![]() 上的函数
上的函数![]() 满足:对任意
满足:对任意![]() ,都有
,都有![]() ,且
,且![]() ;又数列
;又数列![]() 满足
满足![]() .
.
(1)求证: ![]() 是数列
是数列![]() 的母函数;
的母函数;
(2)求数列![]() 的前项
的前项![]() 和
和![]() .
.
(Ⅱ)已知![]() 是数列
是数列![]() 的母函数,且
的母函数,且![]() .若数列
.若数列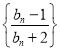 的前
的前![]() 项和为
项和为![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)求证:曲线![]() 在点
在点![]() 处的切线过定点;
处的切线过定点;
(2)若![]() 是
是![]() 在区间
在区间![]() 上的极大值,但不是最大值,求实数
上的极大值,但不是最大值,求实数![]() 的取值范围;
的取值范围;
(3)求证:对任意给定的正数![]() ,总存在
,总存在![]() ,使得
,使得![]() 在
在![]() 上为单调函数.
上为单调函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校大一新生中的6名同学打算参加学校组织的“雅荷文学社”、“青春风街舞社”、“羽乒协会”、“演讲团”、“吉他协会”五个社团,若每名同学必须参加且只能参加1个社团且每个社团至多两人参加,则这6个人中至多有1人参加“演讲团”的不同参加方法数为( )
A. 4680 B. 4770 C. 5040 D. 5200
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列![]() 是无穷数列,且各项均为互不相同的正整数,其前
是无穷数列,且各项均为互不相同的正整数,其前![]() 项和为
项和为![]() ,数列
,数列![]() 满足
满足![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若数列![]() 为等差数列,求
为等差数列,求![]() ;
;
(3)在(1)的条件下,求证:数列![]() 中存在无穷多项(按原来的顺序)成等比数列.
中存在无穷多项(按原来的顺序)成等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂2万元设计了某款式的服装,根据经验,每生产1百套该款式服装的成本为1万元,每生产![]() (百套)的销售额(单位:万元)
(百套)的销售额(单位:万元)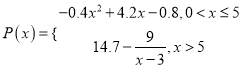 .
.
(1)若生产6百套此款服装,求该厂获得的利润;
(2)该厂至少生产多少套此款式服装才可以不亏本?
(3)试确定该厂生产多少套此款式服装可使利润最大,并求最大利润.(注:利润=销售额-成本,其中成本=设计费+生产成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
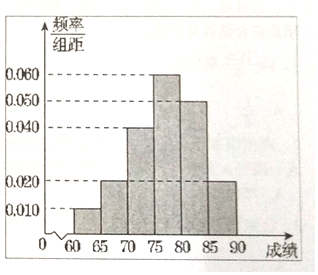
【题目】在某次综合素质测试中,共设有60个考场,每个考场30名考生,在考试结束后,为调查其测试前的培训辅导情况与测试成绩的相关性,抽取每个考场中座位号为06的考生,统计了他们的成绩,得到如图所示的频率分布直方图.
问:
在这个调查采样中,采用的是什么抽样方法?
估计这次测试中优秀(80分及以上)的人数;
写出这60名考生成绩的众数、中位数、平均数的估计值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com