
【题目】比较下列各组数中两个数的大小.
(1) ![]() 与
与![]() ;
;
(2)3![]() 与3.1
与3.1![]() ;
;
(3) 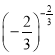 与
与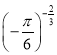 ;
;
(4)0.20.6与0.30.4.
【答案】(1) ![]() >
>![]() (2)3
(2)3![]() >3.1
>3.1![]() (3)
(3)  <
<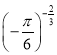 (4)0.20.6<0.30.4.
(4)0.20.6<0.30.4.
【解析】试题分析:(1)借助于函数y=![]() 在(0,+∞)上单调递增,即可比较大小;
在(0,+∞)上单调递增,即可比较大小;
(2)借助于y=![]() 在(0,+∞)上为减函数,即可比较大小;
在(0,+∞)上为减函数,即可比较大小;
(3)借助于中间变量0.20.4,易知0.20.6<0.20.4,0.20.4<0.30.4.
试题解析:
(1)函数y=![]() 在(0,+∞)上单调递增,
在(0,+∞)上单调递增,
又![]() >
>![]() ,∴
,∴ ![]() >
>![]() .
.
(2)y=![]() 在(0,+∞)上为减函数,
在(0,+∞)上为减函数,
又3<3.1,∴3![]() >3.1
>3.1![]()
(3)函数y=![]() 在(0,+∞)上为减函数,
在(0,+∞)上为减函数,
又![]() >
>![]() ,
,
∴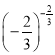 <
<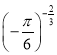 .
.
(4)函数取中间值0.20.4,函数y=0.2x在(0,+∞)上为减函数,所以0.20.6<0.20.4;
又函数y=x0.4在(0,+∞)为增函数,所以0.20.4<0.30.4.
∴0.20.6<0.30.4.
点睛: 本题考查幂函数的图象和性质,属于基础题.幂函数的图象一定在第一象限内,一定不在第四象限,至于是否在第二、三象限内,要看函数的奇偶性;幂函数的图象最多只能同时在两个象限内;如果幂函数图象与坐标轴相交,则交点一定是原点.对于函数f(x)=xα,当![]() 时,函数在
时,函数在![]() 单调递减;当
单调递减;当![]() 时,函数在
时,函数在![]() 单调递增;当
单调递增;当![]() 时,函数为常函数.
时,函数为常函数.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC﹣A1B1C1中,AB=AC=AA1 , AB⊥AC,M是CC1的中点,N是BC的中点,点P在线段A1B1上运动. 
(Ⅰ)求证:PN⊥AM;
(Ⅱ)试确定点P的位置,使直线PN和平面ABC所成的角最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l过点M(3,4),其倾斜角为45°,圆C的参数方程为 ![]() .再以原点为极点,以x正半轴为极轴建立极坐标系,并使得它与直角坐标系xoy有相同的长度单位.
.再以原点为极点,以x正半轴为极轴建立极坐标系,并使得它与直角坐标系xoy有相同的长度单位.
(1)求圆C的极坐标方程;
(2)设圆C与直线l交于点A、B,求|MA||MB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线y=-![]() x+5的倾斜角是直线l的倾斜角的大小的5倍,分别求满足下列条件的直线l的方程.
x+5的倾斜角是直线l的倾斜角的大小的5倍,分别求满足下列条件的直线l的方程.
(1)过点P(3,-4);
(2)在x轴上截距为-2;
(3)在y轴上截距为3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知一艘海监船O上配有雷达,其监测范围是半径为25 km的圆形区域,一艘外籍轮船从位于海监船正东40 km的A处出发,径直驶向位于海监船正北30 km的B处岛屿,速度为28 km/h.
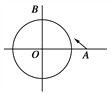
问:这艘外籍轮船能否被海监船监测到?若能,持续时间多长?(要求用坐标法)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设[x]表示不超过x的最大整数,如:[π]=3,[﹣4.3]=﹣5.给出下列命题: ①对任意实数x,都有[x]﹣x≤0;
②若x1≤x2 , 则[x1]≤[x2];
③[lg1]+[lg2]+[lg3]+…+[lg100]=90;
④若函数f(x)= ![]() ﹣
﹣ ![]() ,则y=[f(x)]+[f(﹣x)]的值域为{﹣1,0}.
,则y=[f(x)]+[f(﹣x)]的值域为{﹣1,0}.
其中所有真命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2﹣2ax﹣8a2(a>0),记不等式f(x)≤0的解集为A.
(1)当a=1时,求集合A;
(2)若(﹣1,1)A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,PA⊥平面ABC,AE⊥PB,AB⊥BC,AF⊥PC,PA=AB=BC.
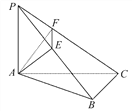
(1)求证:平面AEF⊥平面PBC.
(2)求二面角P-BC-A的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com