
分析 利用不等式的解法、函数的性质分别化简命题p,q.对a分类讨论,利用简易逻辑的判定方法即可得出.
解答 解:由$\frac{4}{x-1}≤-1$解得p:-3≤x<1,
由x2+x<a2-a得(x+a)[x-(a-1)]<0,
当$a=\frac{1}{2}$时,可得q:∅;
当$a<\frac{1}{2}$时,可得q:(a-1,-a);
当$a>\frac{1}{2}$时,可得q:(-a,a-1).
由题意得,p是q的一个必要不充分条件,
当$a=\frac{1}{2}$时,满足条件;当$a<\frac{1}{2}$时,(a-1,-a)?[-3,1)得$a∈[{-1,\frac{1}{2}})$,
当$a>\frac{1}{2}$时,(-a,a-1)?[-3,1)得$a∈({\frac{1}{2},2}]$.
综上,a∈[-1,2].
点评 本题考查了不等式的解法、函数的性质、简易逻辑的判定方法,考查了分类讨论方法、推理能力与计算能力,属于中档题.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:选择题
 如图是根据某校10位高一同学的身高(单位:cm)画出的茎叶图,其中左边的数字从左到右分别表示学生身高的百位数字和十位数字,右边的数字表示学生身高的个位数字,从图中可以得到这10位同学身高的中位数是( )
如图是根据某校10位高一同学的身高(单位:cm)画出的茎叶图,其中左边的数字从左到右分别表示学生身高的百位数字和十位数字,右边的数字表示学生身高的个位数字,从图中可以得到这10位同学身高的中位数是( )| A. | 161 cm | B. | 162 cm | C. | 163 cm | D. | 164 cm |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
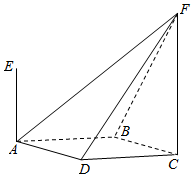 如图,四棱锥F-ABCD的底面ABCD是菱形,其对角线AC=2,BD=$\sqrt{2}$,AE、CF都与平面ABCD垂直,AE=1,CF=2.
如图,四棱锥F-ABCD的底面ABCD是菱形,其对角线AC=2,BD=$\sqrt{2}$,AE、CF都与平面ABCD垂直,AE=1,CF=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 几何题 | 代数题 | 总计 | |
| 男同学 | 22 | 8 | 30 |
| 女同学 | 8 | 12 | 20 |
| 总计 | 30 | 20 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[-1,\sqrt{2}]$ | B. | $[-\sqrt{2},\sqrt{2}]$ | C. | $[\sqrt{2}-2,2]$ | D. | $[1-\sqrt{2},1+\sqrt{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 24 | C. | 48 | D. | 720 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com