
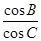 =-
=-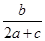 .
.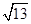 ,a+c=4,求△ABC的面积.
,a+c=4,求△ABC的面积.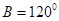 (2)
(2)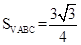
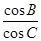 =-
=-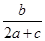 .,得到-sinBcosC=2cosBsinA+cosBsinC(3分)sinBcosC+cosBsinC+2cosBsinA=0,
.,得到-sinBcosC=2cosBsinA+cosBsinC(3分)sinBcosC+cosBsinC+2cosBsinA=0, ,所以B=120°;(7分)(2)由余弦定理得:b2=a2+c2-2accosB,(9分)19=(a+c)2-2ac-2accos120°,所以ac=6,(11分)由a+c=5,ac=6,可得a=2,c=3,或a=3,c=2.,故可知
,所以B=120°;(7分)(2)由余弦定理得:b2=a2+c2-2accosB,(9分)19=(a+c)2-2ac-2accos120°,所以ac=6,(11分)由a+c=5,ac=6,可得a=2,c=3,或a=3,c=2.,故可知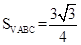 ,
,

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com