(本小题满分13分)
已知函数
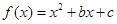
,且
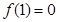
(1)若函数
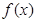
是偶函数,求
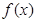
的解析式;
(2)在(1)的条件下,求函数
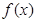
在区间
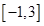
上的最大值和最小值。
(3)要使函数
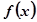
在区间
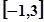
上单调递增,求
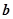
的取值范围.
解:(1)因为函数
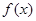
是偶函数,所以b=0,且
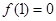
,所以
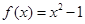
……………4分
(2)结合图像得x=0,
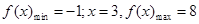
………………………………8分
(3)
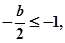
即
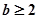
时,
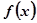
在区间
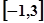
上是递增的.………………13分
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(本题14分)已知
a,
b实数,设函数
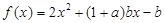
.
(1)若关于
x的不等式
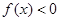
的解集为
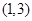
,求实数
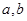
的值;
(2)设
b为已知的常数,且
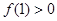
,求满足条件的
a的范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数

(1)当
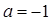
时,求函数的最大值和最小值;
(2)求实数
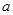
的取值范围,使
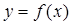
在区间
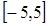
上是单调减函数
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(1)求函数
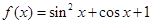
,
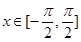
的值域.
(2)求函数
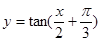
的定义域和单调区间
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
设二次函数
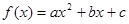
的图象以
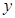
轴

为对称轴,已知
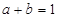
,而且若点
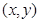
在
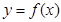
的图象上,则点
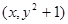
在函数
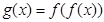
的图象上
(1)求
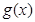
的解析式
(2)设
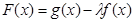
,问是否存在实数
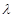
,使
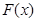
在
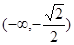
内是减函数,在
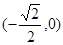
内是增函数。
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
如果函数
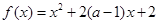
在区间
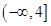
上是单调减函数,那么实数
的取值范围是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知函数
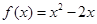
,
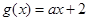
(
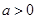
),若
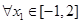
,
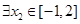
,使得
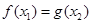
,则实数
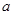
的取值范围是 ( )
查看答案和解析>>

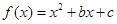 ,且
,且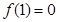
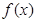 是偶函数,求
是偶函数,求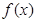 的解析式;
的解析式;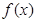 在区间
在区间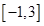 上的最大值和最小值。
上的最大值和最小值。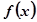 在区间
在区间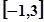 上单调递增,求
上单调递增,求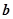 的取值范围.
的取值范围. 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案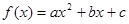 的图象以
的图象以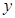 轴
轴 为对称轴,已知
为对称轴,已知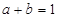 ,而且若点
,而且若点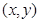 在
在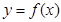 的图象上,则点
的图象上,则点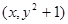 在函数
在函数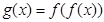 的图象上
的图象上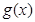 的解析式
的解析式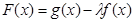 ,问是否存在实数
,问是否存在实数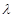 ,使
,使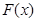 在
在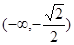 内是减函数,在
内是减函数,在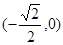 内是增函数。
内是增函数。