
| 3 |
| 5 |
| 9 |
| 20 |
科目:高中数学 来源:不详 题型:解答题
 分别写在大小、形状都相同的
分别写在大小、形状都相同的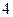 张卡片上,将它们反扣后(数字向下),再从左到右随机的依次摆放,然后从左到右依次翻卡片:若第一次就翻出数字
张卡片上,将它们反扣后(数字向下),再从左到右随机的依次摆放,然后从左到右依次翻卡片:若第一次就翻出数字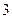 则停止翻卡片;否则就继续翻,若将翻出的卡片上的数字依次相加所得的和是
则停止翻卡片;否则就继续翻,若将翻出的卡片上的数字依次相加所得的和是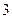 的倍数则停止翻卡片;否则将卡片依次翻完也停止翻卡片.设翻卡片停止时所翻的次数为随机变量
的倍数则停止翻卡片;否则将卡片依次翻完也停止翻卡片.设翻卡片停止时所翻的次数为随机变量 ,求出
,求出 的分布列和它的数学期望.
的分布列和它的数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题


 表示抽取的3名工人中男工人数,求
表示抽取的3名工人中男工人数,求 的分布列及数学期望.
的分布列及数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| ξ | 1 | 2 | 3 | 4 | ||||
| P |
| m | n |
|
A.
| B.
| C.
| D.
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| . |
| x |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com