
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,则称
,则称![]() 是“紧密数列”.
是“紧密数列”.
(1)若数列![]() 是“紧密数列”,且
是“紧密数列”,且![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若![]() 为等差数列,首项
为等差数列,首项![]() ,公差
,公差![]() ,且
,且![]() ,判断
,判断![]() 是否为“紧密数列”,并说明理由;
是否为“紧密数列”,并说明理由;
(3)设数列![]() 是公比为
是公比为![]() 的等比数列,若数列
的等比数列,若数列![]() 与
与![]() 都是“紧密数列”,求
都是“紧密数列”,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() 是“紧密数列”,详见解析(3)
是“紧密数列”,详见解析(3)![]()
【解析】
(1)由 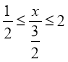 ,
,![]() 可求出
可求出![]() 的取值范围;
的取值范围;
(2)由![]() ,所以
,所以![]()
![]()
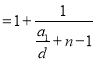
![]() ,根据“紧密数列”的定义即可得到结论;
,根据“紧密数列”的定义即可得到结论;
(3)根据”![]() 是紧密函数”可得
是紧密函数”可得![]() ,再对
,再对![]() 分
分![]() 三种情况套,结合“紧密数列”的定义可得.
三种情况套,结合“紧密数列”的定义可得.
(1)由题意得: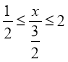 ,
,![]() ,解得
,解得![]() .
.
所以![]() 的取值范围是
的取值范围是![]() .
.
(2)由题意得![]() ,所以
,所以![]()
![]()
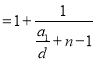
![]() ,
,
因为![]() 随着
随着![]() 的增大而减小,所以
的增大而减小,所以![]() 时,
时,![]() 取得最大值,所以
取得最大值,所以 ,
,
所以![]() 是“紧密数列”.
是“紧密数列”.
(3)由数列![]() 是公比为
是公比为![]() 的等比数列,得
的等比数列,得![]() ,
,
因为![]() 是“紧密数列”,所以
是“紧密数列”,所以![]() .
.
①当![]() 时,
时,![]() ,
,![]() ,因为
,因为![]() ,所以
,所以![]() 时,数列
时,数列![]() 为“紧密数列”,故
为“紧密数列”,故![]() 满足题意.
满足题意.
②当![]() 时,
时,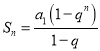 ,则
,则![]() ,因为数列
,因为数列![]() 为“紧密数列”,
为“紧密数列”,
所以![]() ,对任意
,对任意![]() 恒成立.
恒成立.
(i)当![]() 时,
时,![]() ,
,
即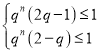 ,对任意
,对任意![]() 恒成立.
恒成立.
因为![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
所以,当![]() 时,
时,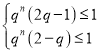 ,对任意
,对任意![]() 恒成立.
恒成立.
(ii)当![]() 时,
时,![]() ,即
,即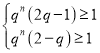 ,对任意
,对任意![]() 恒成立.
恒成立.
所以当![]() 时,有
时,有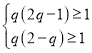 成立,即
成立,即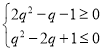 ,所以
,所以![]() 且
且![]() ,
,
所以![]() ,这与
,这与![]() 相矛盾,此时
相矛盾,此时![]() 不存在.
不存在.
综上所述,![]() 的取值范围是
的取值范围是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,以线段
,以线段![]() 为直径的圆与椭圆交于点
为直径的圆与椭圆交于点 .
.

(1)求椭圆的方程;
(2)过![]() 轴正半轴上一点
轴正半轴上一点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() .
.
①若![]() 与圆和椭圆都相切,求实数
与圆和椭圆都相切,求实数![]() 的值;
的值;
②直线![]() 在
在![]() 轴左侧交圆于
轴左侧交圆于![]() 、
、![]() 两点,与椭圆交于点
两点,与椭圆交于点![]() 、
、![]() (从上到下依次为
(从上到下依次为![]() 、
、![]() 、
、![]() 、
、![]() ),且
),且![]() ,求实数
,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某饮料生产企业为了占有更多的市场份额,拟在2017年度进行一系列促销活动,经过市场调查和测算,饮料的年销售量x万件与年促销费t万元间满足![]() .已知2017年生产饮料的设备折旧,维修等固定费用为3万元,每生产1万件饮料需再投入32万元的生产费用,若将每件饮料的售价定为其生产成本的150%与平均每件促销费的一半之和,则该年生产的饮料正好能销售完.
.已知2017年生产饮料的设备折旧,维修等固定费用为3万元,每生产1万件饮料需再投入32万元的生产费用,若将每件饮料的售价定为其生产成本的150%与平均每件促销费的一半之和,则该年生产的饮料正好能销售完.
(1)将2017年的利润y(万元)表示为促销费t(万元)的函数;
(2)该企业2017年的促销费投入多少万元时,企业的年利润最大?
(注:利润=销售收入-生产成本-促销费,生产成本=固定费用+生产费用)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.在如图所示的阳马![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,且
,且![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() 、
、![]() 、
、![]() .
.
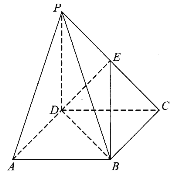
(1)证明:![]() 平面
平面![]() ;
;
(2)证明:![]() 平面
平面![]() .试判断四面体
.试判断四面体![]() 是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,请说明理由;
是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,请说明理由;
(3)记阳马![]() 的体积为
的体积为![]() ,四面体
,四面体![]() 的体积为
的体积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式
的通项公式![]() ;
;
(2)设![]() ,若对一切正整数
,若对一切正整数![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;.
的取值范围;.
(3)是否存在正整数![]() ,使得
,使得![]() 。成等比数列?若存在,求出所有的
。成等比数列?若存在,求出所有的![]() ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]()
(1)若函数f(x)有两个零点,求实数a的取值范围;
(2)若a=3,且对任意的x1∈[-1,2],总存在![]() ,使g(x1)-f(x2)=0成立,求实数m的取值范围.
,使g(x1)-f(x2)=0成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某租车公司给出的财务报表如下:
年度 项目 | 2014年 (1-12月) | 2015年 (1-12月) | 2016年 (1-11月) |
接单量(单) | 14463272 | 40125125 | 60331996 |
油费(元) | 214301962 | 581305364 | 653214963 |
平均每单油费 | 14.82 | 14.49 | |
平均每单里程 | 15 | 15 | |
每公里油耗 | 0.7 | 0.7 | 0.7 |
有投资者在研究上述报表时,发现租车公司有空驶情况,并给出空驶率的计算公式为![]() .
.
(1)分别计算2014,2015年该公司的空驶率的值(精确到0.01%);
(2)2016年该公司加强了流程管理,利用租车软件,降低了空驶率并提高了平均每单里程,核算截止到11月30日,空驶率在2015年的基础上降低了20个百分点,问2016年前11个月的平均每单油费和平均每单里程分别为多少?(分别精确到0.01元和0.01公里).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 由方程
由方程![]() 确定,下列结论正确的是________(请将你认为正确的序号都填上)
确定,下列结论正确的是________(请将你认为正确的序号都填上)
① ![]() 是
是![]() 上的单调递减函数;
上的单调递减函数;
② 对于任意![]() ,
,![]() 恒成立;
恒成立;
③ 对于任意![]() ,关于
,关于![]() 的方程
的方程![]() 都有解;
都有解;
④ ![]() 存在反函数
存在反函数![]() ,且对任意
,且对任意![]() ,总有
,总有![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,长轴长为
,长轴长为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程及离心率;
的标准方程及离心率;
(Ⅱ)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,若点
两点,若点![]() 满足
满足![]() ,求证:由点
,求证:由点![]() 构成的曲线
构成的曲线![]() 关于直线
关于直线![]() 对称.
对称.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com