
| A�� | 1-$\sqrt{2}$ | B�� | $\sqrt{2}$-1 | C�� | 5-$\sqrt{2}$ | D�� | $\sqrt{2}$-5 |
���� ���ݷֶκ������溯�������ʷֱ����ÿ���ϵ���㣬������ͼ��ɣ�
��� �⣺��x��1ʱ��
��1-|x-3|+$\frac{1}{2}$=0�����x=$\frac{9}{2}$����x=$\frac{3}{2}$��
��0��x��1ʱ����log${\;}_{\frac{1}{2}}$��x+1��+$\frac{1}{2}$=0�����x=$\sqrt{2}$-1��
��f��x��Ϊ�溯����
�൱-1��x��0ʱ��f��x��=-log${\;}_{\frac{1}{2}}$��-x+1������-log${\;}_{\frac{1}{2}}$��-x+1��+$\frac{1}{2}$=0�����x=1-$\frac{\sqrt{2}}{2}$����ȥ����
��x��-1ʱ��f��x��=-1+|x+3|����-1+|x+3|+$\frac{1}{2}$=0�����x=-$\frac{7}{2}$��x=-$\frac{5}{2}$��
�����е����֮��Ϊ$\frac{9}{2}$+$\frac{3}{2}$+$\sqrt{2}$-1-$\frac{7}{2}$-$\frac{5}{2}$=$\sqrt{2}$-1��
��ѡ��B
���� ���⿼���˺��������ͷֶκ����Լ��溯�������ʣ������е��⣮


 �����ܾ�ϵ�д�
�����ܾ�ϵ�д� ���ƿ�����ϵ�д�
���ƿ�����ϵ�д� ���¿쳵����������ϵ�д�
���¿쳵����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ABCD-A1B1C1D1�������壬O��M��N�ֱ���B1D1��AB1��AD1���е㣬ֱ��A1C��ƽ��AB1D1�ڵ�P��
��ͼ��ABCD-A1B1C1D1�������壬O��M��N�ֱ���B1D1��AB1��AD1���е㣬ֱ��A1C��ƽ��AB1D1�ڵ�P���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{6}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{1}{3}$ | D�� | $\frac{1}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��x+�� | 0 | $\frac{��}{2}$ | �� | $\frac{3��}{2}$ | 2�� |
| x | $\frac{��}{3}$ | $\frac{5��}{6}$ | |||
| Asin����x+�գ� | 0 | 2 | -2 | 0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 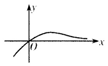 | B�� |  | C�� |  | D�� | 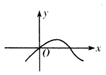 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com