
【题目】如图,在多面体![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
,![]() .
.
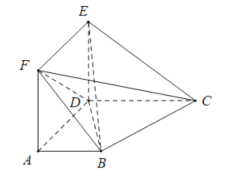
(1)证明:![]() 平面
平面![]() ;
;
(2)若二面角![]() 的正弦值为
的正弦值为![]() ,求
,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】随着经济模式的改变,微商和电商已成为当今城乡一种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,没售出1吨该商品可获利润0.5万元,未售出的商品,每1吨亏损0.3万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了130吨该商品,现以![]() (单位:吨,
(单位:吨,![]() )表示下一个销售季度的市场需求量,
)表示下一个销售季度的市场需求量,![]() (单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
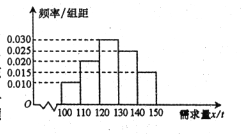
(Ⅰ)视![]() 分布在各区间内的频率为相应的概率,求
分布在各区间内的频率为相应的概率,求![]() ;
;
(Ⅱ)将![]() 表示为
表示为![]() 的函数,求出该函数表达式;
的函数,求出该函数表达式;
(Ⅲ)在频率分布直方图的市场需求量分组中,以各组的区间中点值(组中值)代表该组的各个值,并以市场需求量落入该区间的频率作为市场需求量取该组中值的概率(例如![]() ,则取
,则取![]() 的概率等于市场需求量落入
的概率等于市场需求量落入![]() 的频率),求
的频率),求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系.直线
轴正半轴为极轴建立极坐标系.直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程与直线
的极坐标方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且点
上,且点![]() 到点
到点![]() 的最大距离为
的最大距离为![]() ,点
,点![]() 到点
到点![]() 的最小距离为
的最小距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,坐标原点
两点,坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,点P为抛物线C上一点,
的焦点为F,点P为抛物线C上一点,![]() ,O为坐标原点,
,O为坐标原点,![]() .
.
(1)求抛物线C的方程;
(2)设Q为抛物线C的准线上一点,过点F且垂直于OQ的直线交抛物线C于A,B两点记![]() ,
,![]() 的面积分别为
的面积分别为![]()
![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为![]() (φ为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2是圆心为(2,
(φ为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2是圆心为(2,![]() ),半径为1的圆.
),半径为1的圆.
(1)求曲线C1的普通方程和C2的直角坐标方程;
(2)设M为曲线C1上的点,N为曲线C2上的点,求|MN|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知常数a≠0,数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]()
(1)求证:数列![]() 为等差数列;
为等差数列;
(2)若![]() 且数列
且数列![]() 是单调递增数列,求实数a的取值范围;
是单调递增数列,求实数a的取值范围;
(3)若![]() 数列
数列![]() 满足:
满足: ![]() 对于任意给定的正整数k,是否存在p,
对于任意给定的正整数k,是否存在p,![]() ,使
,使![]() 若存在,求p,q的值(只要写出一组即可);若不存在,说明理由.
若存在,求p,q的值(只要写出一组即可);若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 的焦点,点
的焦点,点![]() 在
在![]() 轴上,
轴上,![]() 为坐标原点,且满足
为坐标原点,且满足![]() ,经过点
,经过点![]() 且垂直于
且垂直于![]() 轴的直线与抛物线
轴的直线与抛物线![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求点
,求点![]() 到直线
到直线![]() 的最大距离.
的最大距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,面CDEF为正方形,平面ABCD为等腰梯形,AB//CD,AB =2BC,点Q为AE的中点.

(1)求证:AC//平面DQF;
(2)若∠ABC=60°,AC⊥FB,求BC与平面DQF所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com