
分析 (1)由PF2⊥x轴,先求出点P的坐标,再由PF2∥AB,能得到b=2c,由此能求出椭圆的离心率.
(2)把x=c代入椭圆方程可得A(c,$\frac{{b}^{2}}{a}$),B(c,-$\frac{{b}^{2}}{a}$).由$\overline{OA}$•$\overline{OB}$=0,可得c2-($\frac{{b}^{2}}{a}$)2=0,即可求椭圆的离心率.
解答 解:(1)∵PF2⊥x轴,∴点P的坐标(c,$\frac{{b}^{2}}{a}$),
kAB=$\frac{b}{a}$,${k}_{P{F}_{2}}$=$\frac{{b}^{2}}{2ac}$,
∵PF2∥AB,
∴kAB=${k}_{P{F}_{2}}$,即$\frac{b}{a}$=$\frac{{b}^{2}}{2ac}$,
整理,得b=2c,
∴a2=b2+c2=5c2,即a=$\sqrt{5}$c,
∴e=$\frac{c}{a}$=$\frac{\sqrt{5}}{5}$.
(2)把x=c代入椭圆方程可得y=±$\frac{{b}^{2}}{a}$.
取A(c,$\frac{{b}^{2}}{a}$),B(c,-$\frac{{b}^{2}}{a}$).
∵$\overline{OA}$•$\overline{OB}$=0,
∴c2-($\frac{{b}^{2}}{a}$)2=0,
化为ac-(a2-c2)=0,
∴e2+e-1=0,0<e<1,
解得e=$\frac{\sqrt{5}-1}{2}$.
点评 本题考查椭圆的离心率,考查了推理能力与计算能力,解题时要熟练掌握椭圆的简单性质,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{8}$,0)∪(0,+∞) | B. | (-$\frac{1}{8}$,+∞) | C. | (-∞,0)∪(0,$\frac{1}{8}$) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{1004}$ | B. | 1004 | C. | 2$\sqrt{2008}$ | D. | 2008 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
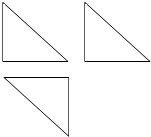 如图,一个几何体的三视图是三个全等的等腰直角三角形,且直角边长为2,则这个几何体的外接球的表面积为( )
如图,一个几何体的三视图是三个全等的等腰直角三角形,且直角边长为2,则这个几何体的外接球的表面积为( )| A. | 16π | B. | 12π | C. | 8π | D. | 4π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com