
【题目】某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价为5元,销售单价与日均销售量的关系如图所示.
销售单价/元 | … | 6 | 6.5 | 7 | 7.5 | 8 | 8.5 | … |
日均销售量/桶 | … | 480 | 460 | 440 | 420 | 400 | 380 | … |
请根据以上数据作出分析,这个经营部怎样定价才能获得最大利润?
 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】阿波罗尼斯是古希腊著名数学家,与欧几里得、阿基米德被称为亚历山大时期数学三巨匠,他对圆锥曲线有深刻而系统的研究,主要研究成果集中在他的代表作《圆锥曲线》一书,阿波罗尼斯圆是他的研究成果之一,指的是:已知动点M与两定点A、B的距离之比为λ(λ>0,λ≠1),那么点M的轨迹就是阿波罗尼斯圆.下面,我们来研究与此相关的一个问题.已知圆:x2+y2=1和点 ![]() ,点B(1,1),M为圆O上动点,则2|MA|+|MB|的最小值为( )
,点B(1,1),M为圆O上动点,则2|MA|+|MB|的最小值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() 的离心率为e,经过第一、三象限的渐近线的斜率为k,且e≥
的离心率为e,经过第一、三象限的渐近线的斜率为k,且e≥ ![]() k.
k.
(1)求m的取值范围;
(2)设条件p:e≥ ![]() k;条件q:m2﹣(2a+2)m+a(a+2)≤0.若p是q的必要不充分条件,求a的取值范围.
k;条件q:m2﹣(2a+2)m+a(a+2)≤0.若p是q的必要不充分条件,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,三棱柱A1B1C1﹣ABC的侧棱AA1⊥底面ABC,AB⊥AC,AB=AA1 , D是棱CC1的中点.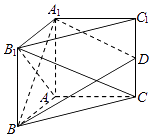
(Ⅰ)证明:平面AB1C⊥平面A1BD;
(Ⅱ)在棱A1B1上是否存在一点E,使C1E∥平面A1BD?并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正四棱锥![]() 中,
中, ![]() 是正方形,
是正方形, ![]() 是正方形的中心,
是正方形的中心, ![]() 底面
底面![]() ,
, ![]() 是
是![]() 的中点.
的中点.
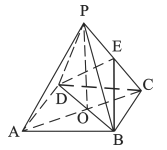
(I)证明: ![]() 平面
平面![]() ;
;
(II)证明:平面![]() 平面
平面![]() ;
;
(III)已知: ![]() ,求点
,求点![]() 到面
到面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解1000名高一新生的身体生长状况,用系统抽样法(按等距的规则)抽取40名同学进行检查,将学生从1~1000进行编号,现已知第18组抽取的号码为443,则第一组用简单随机抽样抽取的号码为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() 在线段
在线段![]() 上,
上, ![]() ,
, ![]() .
.
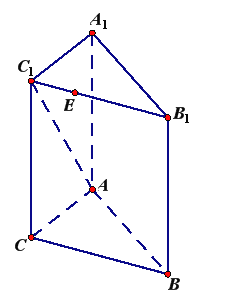
(1)求证: ![]() ;
;
(2)试探究:在![]() 上是否存在点
上是否存在点![]() ,满足
,满足![]() 平面
平面![]() ,若存在,请指出点
,若存在,请指出点![]() 的位置,并给出证明;若不存在,说明理由.
的位置,并给出证明;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱柱ABC﹣A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2 ![]() ,D是AA1的中点,BD与AB1交于点O,且CO⊥平面ABB1A1 .
,D是AA1的中点,BD与AB1交于点O,且CO⊥平面ABB1A1 . 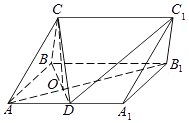
(1)证明:CD⊥AB1;
(2)若OC=OA,求直线CD与平面ABC所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com