
【题目】对于定义域为![]() 的函数
的函数![]() ,如果存在区间
,如果存在区间![]() (
(![]() ),同时满足:
),同时满足:
①![]() 在
在![]() 内是单调函数;②当定义域是
内是单调函数;②当定义域是![]() 时,
时, ![]() 的值域也是
的值域也是![]() .
.
则称函数![]() 是区间
是区间![]() 上的“保值函数”.
上的“保值函数”.
(1)求证:函数![]() 不是定义域
不是定义域![]() 上的“保值函数”;
上的“保值函数”;
(2)已知![]() (
(![]() )是区间
)是区间![]() 上的“保值函数”,求
上的“保值函数”,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】设函数f(x)=(x3﹣1)2+1,下列结论中正确的是( )
A.x=1是函数f(x)的极小值点,x=0是函数f(x)的极大值点
B.x=1及x=0均是函数f(x)的极大值点
C.x=1是函数f(x)的极大值点,x=0是函数f(x)的极小值点
D.x=1是函数f(x)的极小值点,函数f(x)无极大值点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数fn(x)=xn+bx+c(n∈N* , b,c∈R)
(Ⅰ)设n≥2,b=1,c=﹣1,证明:fn(x)在区间( ![]() )内存在唯一的零点;
)内存在唯一的零点;
(Ⅱ)设n=2,若对任意x1 , x2∈[﹣1,1],均有|f2(x1)﹣f2(x2)丨≤4,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:方程 ![]() =1所表示的图形是焦点在y轴上的双曲线,命题q:复数z=(m﹣3)+(m﹣1)i对应的点在第二象限,又p或q为真,p且q为假,求实数m的取值范围.
=1所表示的图形是焦点在y轴上的双曲线,命题q:复数z=(m﹣3)+(m﹣1)i对应的点在第二象限,又p或q为真,p且q为假,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中正确的序号是 .
①函数y=ax(a>0且a≠1)与函数 ![]() (a>0且a≠1)的定义域相同;
(a>0且a≠1)的定义域相同;
②函数y=k3x(k>0)(k为常数)的图象可由函数y=3x的图象经过平移得到;
③函数 ![]() (x≠0)是奇函数且函数
(x≠0)是奇函数且函数 ![]() (x≠0)是偶函数;
(x≠0)是偶函数;
④若x1是函数f(x)的零点,且m<x1<n,则f(m)f(n)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】春节期间,“厉行节约,反对浪费”之风悄然吹开,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表:
做不到“光盘” | 能做到“光盘” | |
男 | 45 | 10 |
女 | 30 | 15 |
P(K2≥k) | 0.10 | 0.05 | 0.025 |
k | 2.706 | 3.841 | 5.024 |
附: ![]()
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过l%的前提下,认为“该市居民能否做到‘光盘’与性别有关”
B.在犯错误的概率不超过l%的前提下,认为“该市居民能否做到‘光盘’与性别无关”
C.有90%以上的把握认为“该市居民能否做到‘光盘’与性别有关”
D.有90%以上的把握认为“该市居民能否做到‘光盘’与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,焦点在x轴上的椭圆C: ![]() 经过点(b,2e),其中e为椭圆C的离心率.过点T(1,0)作斜率为k(k>0)的直线l交椭圆C于A,B两点(A在x轴下方).
经过点(b,2e),其中e为椭圆C的离心率.过点T(1,0)作斜率为k(k>0)的直线l交椭圆C于A,B两点(A在x轴下方).
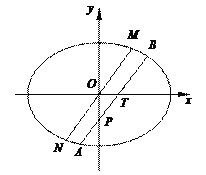
(1)求椭圆C的标准方程;
(2)过点O且平行于l的直线交椭圆C于点M,N,求 ![]() 的值;
的值;
(3)记直线l与y轴的交点为P.若![]() ,求直线l的斜率k.
,求直线l的斜率k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数z=k﹣2i(k∈R)的共轭复数 ![]() ,且z﹣(
,且z﹣( ![]() ﹣i)=
﹣i)= ![]() ﹣2i.
﹣2i.
(1)求k的值;
(2)若过点(0,﹣2)的直线l的斜率为k,求直线l与曲线y= ![]() 以及y轴所围成的图形的面积.
以及y轴所围成的图形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com