
【题目】已知函数![]()
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)谈论函数![]() 的零点个数
的零点个数
【答案】(1) ![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() (2)见解析
(2)见解析
【解析】
(1)求出函数的导数,解关于导函数不等式,求出函数的单调区间;
(2)由(1)知当![]() 时,
时,![]() ,分
,分![]() ,
,![]() ,
,![]() 三种情况讨论,
三种情况讨论,![]() 由函数的定义域为
由函数的定义域为![]() 显然没有零点,当
显然没有零点,当![]() 转化为函数的交点问题.
转化为函数的交点问题.
解:(1)∵![]() ,
,
故![]() ,
,
∵![]()
∴![]() 时,
时,![]() ,故
,故![]() 单调递减,
单调递减,
![]() 时,
时,![]() ,故
,故![]() 单调递增,
单调递增,
所以,![]() 时,
时,![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]()
(2)由(1)知,
当![]() 时,
时,![]() 在
在![]() 处取最小值
处取最小值![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在其定义域内无零点
在其定义域内无零点
当![]() 时,
时,![]() ,
,![]() 在其定义域内恰有一个零点
在其定义域内恰有一个零点
当![]() 时,最小值
时,最小值![]() ,因为
,因为![]() ,且
,且![]() 在
在![]() 单调递减,故函数
单调递减,故函数![]() 在
在![]() 上有一个零点,
上有一个零点,
因为![]() ,
,![]() ,
,![]() ,又
,又![]() 在
在![]() 上单调递增,故函数
上单调递增,故函数![]() 在
在![]() 上有一个零点,故
上有一个零点,故![]() 在其定义域内有两个零点;
在其定义域内有两个零点;
当![]() 时,
时,![]() 在定义域
在定义域![]() 内无零点;
内无零点;
当![]() 时,令
时,令![]() ,可得
,可得![]() ,分别画出
,分别画出![]() 与
与![]() ,易得它们的图象有唯一交点,即此时
,易得它们的图象有唯一交点,即此时![]() 在其定义域内恰有一个零点
在其定义域内恰有一个零点
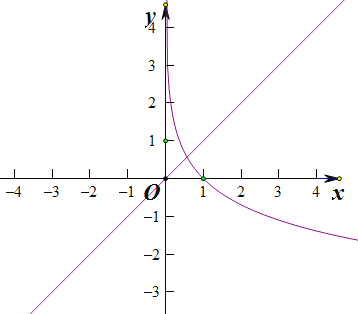
综上,![]() 时,
时,![]() 在其定义域内无零点;
在其定义域内无零点;![]() 或
或![]() 时,
时,![]() 在其定义域内恰有一个零点;
在其定义域内恰有一个零点;![]() 时,
时,![]() 在其定义域内有两个零点;
在其定义域内有两个零点;


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:高中数学 来源: 题型:
【题目】下列四个命题中真命题是![]()
![]()
A. 同垂直于一直线的两条直线互相平行
B. 底面各边相等,侧面都是矩形的四棱柱是正四棱柱
C. 过空间任一点与两条异面直线都垂直的直线有且只有一条
D. 过球面上任意两点的大圆有且只有一个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() .
.

(Ⅰ)求证:![]() ;
;
(Ⅱ)是否存在实数![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求出实数
?若存在,求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2011年国际数学协会正式宣布,将每年的3月14日设为国际数学节,来源于中国古代数学家祖冲之的圆周率。公元263年,中国数学家刘徽用“割圆术”计算圆周率,计算到圆内接3072边形的面积,得到的圆周率是![]() .公元480年左右,南北朝时期的数学家祖冲之进一步得出精确到小数点后7位的结果,给出不足近似值3.1415926和过剩近似值3.1415927,还得到两个近似分数值,密率
.公元480年左右,南北朝时期的数学家祖冲之进一步得出精确到小数点后7位的结果,给出不足近似值3.1415926和过剩近似值3.1415927,还得到两个近似分数值,密率![]() 和约率
和约率![]() 。大约在公元530年,印度数学大师阿耶波多算出圆周率约为
。大约在公元530年,印度数学大师阿耶波多算出圆周率约为![]() (
(![]() ).在这4个圆周率的近似值中,最接近真实值的是( )
).在这4个圆周率的近似值中,最接近真实值的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列A:![]() ,
,![]() ,…
,…![]() (
(![]() ).如果对小于
).如果对小于![]() (
(![]() )的每个正整数
)的每个正整数![]() 都有
都有![]() <
<![]() ,则称
,则称![]() 是数列A的一个“G时刻”.记“
是数列A的一个“G时刻”.记“![]() 是数列A的所有“G时刻”组成的集合.
是数列A的所有“G时刻”组成的集合.
(1)对数列A:-2,2,-1,1,3,写出![]() 的所有元素;
的所有元素;
(2)证明:若数列A中存在![]() 使得
使得![]() >
>![]() ,则
,则![]() ;
;
(3)证明:若数列A满足![]() -
-![]() ≤1(n=2,3, …,N),则
≤1(n=2,3, …,N),则![]() 的元素个数不小于
的元素个数不小于![]() -
-![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某篮球教练对甲乙两位运动员在近五场比赛中的得分情况统计如下图所示,根据图表给出如下结论:(1)甲乙两人得分的平均数相等且甲的方差比乙的方差小;(2)甲乙两人得分的平均数相等且甲的方差比乙的方差大;(3)甲的成绩在不断提高,而乙的成绩无明显提高;(4)甲的成绩较稳定,乙的成续基本呈上升状态;结论正确的是( )
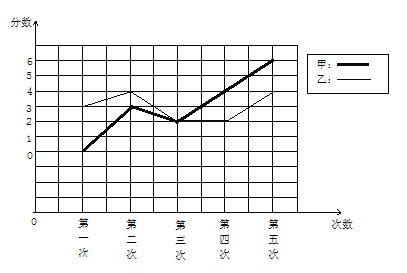
A.(1)(3)B.(1)(4)C.(2)(3)D.(2)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数![]() 的定义域为
的定义域为![]() ,且存在实常数a,使得对于定义域内任意x,都
,且存在实常数a,使得对于定义域内任意x,都![]() 成立,则称此函数
成立,则称此函数![]() 具有“
具有“![]() 性质”
性质”
(1)判断函数![]() 是否具有“
是否具有“![]() 性质”,若具有“
性质”,若具有“![]() 性质”,求出所有a的值的集合;若不具有“
性质”,求出所有a的值的集合;若不具有“![]() 性质”,请说明理由;
性质”,请说明理由;
(2)已知函数![]() 具有“
具有“![]() 性质”,且当
性质”,且当![]() 时,
时,![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的值域;
上的值域;
(3)已知函数![]() 具有“
具有“![]() 性质”,又具有“
性质”,又具有“![]() 性质”,且当
性质”,且当![]() 时,
时,![]() ,若函数
,若函数![]() 的图像与直线
的图像与直线![]() 有2017个公共点,求实数p的值.
有2017个公共点,求实数p的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,且点
,且点![]() 在椭圆C上.
在椭圆C上.
(1)求椭圆C的标准方程;
(2)过椭圆 上异于其顶点的任意一点Q作圆
上异于其顶点的任意一点Q作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() 不在坐标轴上),若直线
不在坐标轴上),若直线![]() 在x轴,y轴上的截距分别为
在x轴,y轴上的截距分别为![]() ,证明:
,证明:![]() 为定值;
为定值;
(3)若![]() 是椭圆
是椭圆![]() 上不同两点,
上不同两点,![]() 轴,圆E过
轴,圆E过![]() ,且椭圆
,且椭圆![]() 上任意一点都不在圆E内,则称圆E为该椭圆的一个内切圆,试问:椭圆
上任意一点都不在圆E内,则称圆E为该椭圆的一个内切圆,试问:椭圆![]() 是否存在过焦点F的内切圆?若存在,求出圆心E的坐标;若不存在,请说明理由.
是否存在过焦点F的内切圆?若存在,求出圆心E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校组织了垃圾分类知识竞赛活动.设置了四个箱子,分别写有“厨余垃圾”、“有害垃圾”、“可回收物”、“其它垃圾”;另有卡片若干张,每张卡片上写有一种垃圾的名称.每位参赛选手从所有卡片中随机抽取![]() 张,按照自己的判断,将每张卡片放入对应的箱子中.按规则,每正确投放一张卡片得
张,按照自己的判断,将每张卡片放入对应的箱子中.按规则,每正确投放一张卡片得![]() 分,投放错误得
分,投放错误得![]() 分.比如将写有“废电池”的卡片放入写有“有害垃圾”的箱子,得
分.比如将写有“废电池”的卡片放入写有“有害垃圾”的箱子,得![]() 分,放入其它箱子,得
分,放入其它箱子,得![]() 分.从所有参赛选手中随机抽取
分.从所有参赛选手中随机抽取![]() 人,将他们的得分按照
人,将他们的得分按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组,绘成频率分布直方图如图:
分组,绘成频率分布直方图如图:
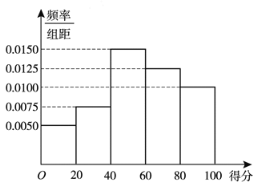
(1)分别求出所抽取的![]() 人中得分落在组
人中得分落在组![]() 和
和![]() 内的人数;
内的人数;
(2)从所抽取的![]() 人中得分落在组
人中得分落在组![]() 的选手中随机选取
的选手中随机选取![]() 名选手,以
名选手,以![]() 表示这
表示这![]() 名选手中得分不超过
名选手中得分不超过![]() 分的人数,求
分的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3) 如果某选手将抽到的20张卡片逐一随机放入四个箱子,能否认为该选手不会得到100分?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com