
【题目】椭圆mx2+ny2=1与直线x+y﹣1=0相交于A,B两点,过AB中点M与坐标原点的直线的斜率为 ![]() ,则
,则 ![]() 的值为( )
的值为( )
A.![]()
B.![]()
C.1
D.2
【答案】A
【解析】解:设A(x1 , y1),B(x2 , y2),M(x0 , y0),
∴ ![]() ①,
①,
kAB= ![]() ②,
②,
由AB的中点为M可得x1+x2=2x0 , y1+y2=2y0
由A,B在椭圆上,可得 ![]() ,
,
两式相减可得m(x1﹣x2)(x1+x2)+n(y1﹣y2)(y1+y2)=0③,
把①②代入③可得m(x1﹣x2)2x0﹣n(x1﹣x2)2y0=0③,
整理可得 ![]()
故选A
(法二)设A(x1 , y1),B(x2 , y2),M(x0 , y0)
联立方程 ![]() 可得(m+n)x2﹣2nx++n﹣1=0
可得(m+n)x2﹣2nx++n﹣1=0
∴x1+x2= ![]() ,y1+y2=2﹣(x1+x2)=
,y1+y2=2﹣(x1+x2)= ![]()
由中点坐标公式可得, ![]() =
= ![]() ,
, ![]() =
= ![]()
∵M与坐标原点的直线的斜率为 ![]()
∴  =
= ![]()
故选A


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:
【题目】【2017湖南娄底二模】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等级如下表:
质量指标值 |
|
|
|
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
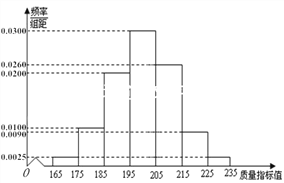
(Ⅰ)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品92%”的规定?
(Ⅱ)在样本中,按产品等级用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(Ⅲ)该企业为提高产品质量,开展了“质量提升月”活动,活动后在抽样检测,产品质量指标值![]() 近似满足
近似满足![]() ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,已知bcos2 ![]() +acos2
+acos2 ![]() =
= ![]() c.
c.
(Ⅰ)求证:a,c,b成等差数列;
(Ⅱ)若C= ![]() ,△ABC的面积为2
,△ABC的面积为2 ![]() ,求c.
,求c.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为备战![]() 年瑞典乒乓球世界锦标赛,乒乓球队举行公开选拨赛,甲、乙、丙三名选手入围最终单打比赛名单.现甲、乙、丙三人进行队内单打对抗比赛,每两人比赛一场,共赛三场,每场比赛胜者得
年瑞典乒乓球世界锦标赛,乒乓球队举行公开选拨赛,甲、乙、丙三名选手入围最终单打比赛名单.现甲、乙、丙三人进行队内单打对抗比赛,每两人比赛一场,共赛三场,每场比赛胜者得![]() 分,负者得
分,负者得![]() 分,在每一场比赛中,甲胜乙的概率为
分,在每一场比赛中,甲胜乙的概率为![]() ,丙胜甲的概率为
,丙胜甲的概率为![]() ,乙胜丙的概率为
,乙胜丙的概率为![]() ,且各场比赛结果互不影响.若甲获第一名且乙获第三名的概率为
,且各场比赛结果互不影响.若甲获第一名且乙获第三名的概率为![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)设在该次对抗比赛中,丙得分为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①已知集合A={1,a},B={1,2,3},则“a=3”是“AB”的充分不必要条件;
②“x<0”是“ln(x+1)<0”的必要不充分条件;
③“函数f(x)=cos2ax﹣sin2ax的最小正周期为π”是“a=1”的充要条件;
④“平面向量 ![]() 与
与 ![]() 的夹角是钝角”的充要条件的“
的夹角是钝角”的充要条件的“ ![]()
![]() <0”.
<0”.
其中正确命题的序号是(把所有正确命题的序号都写上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)
如图,2015年春节,摄影爱好者![]() 在某公园
在某公园![]() 处,发现正前方
处,发现正前方![]() 处有一立柱,测得立柱顶端
处有一立柱,测得立柱顶端![]() 的仰角和立柱底部
的仰角和立柱底部![]() 的俯角均为
的俯角均为![]() ,已知
,已知![]() 的身高约为
的身高约为![]() 米(将眼睛距地面的距离按
米(将眼睛距地面的距离按![]() 米处理)
米处理)

(1)求摄影者到立柱的水平距离和立柱的高度;
(2)立柱的顶端有一长2米的彩杆![]() 绕中点
绕中点![]() 在
在![]() 与立柱所在的平面内旋转.摄影者有一视角范围为
与立柱所在的平面内旋转.摄影者有一视角范围为![]() 的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由.
的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=asinx﹣bcosx的一条对称轴为x= ![]() ,则直线l:ax﹣by+c=0的倾斜角为( )
,则直线l:ax﹣by+c=0的倾斜角为( )
A.45°
B.60°
C.120°
D.135°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com