
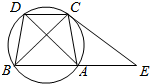
 如图,已知圆中$\widehat{AC}$=$\widehat{BD}$,AC=CD,过C点的圆的切线与BA的延长线交于E点.
如图,已知圆中$\widehat{AC}$=$\widehat{BD}$,AC=CD,过C点的圆的切线与BA的延长线交于E点.分析 (1)证明∠ACE=∠DAC,即可证明AD∥CE
(2)证明△DCA∽△BCE,可得$\frac{DC}{BC}=\frac{AC}{CE}$,即可证明CD•CE=BC•AC.
解答 证明:(1)因为EC与圆相切于点C,
故∠ACE=∠ABC=∠ADC
因为AC=CD,
所以∠DAC=∠ADC.
所以∠ACE=∠DAC.
所以AD∥CE
(2)因为$\widehat{AC}$=$\widehat{BD}$,AC=CD,
所以∠DAB=∠DAC
因为∠DAB=∠CEA,
所以∠CEA=∠DAC,
因为∠CDA=∠CBA,
所以△DCA∽△BCE,
所以$\frac{DC}{BC}=\frac{AC}{CE}$
所以CD•CE=BC•AC.
点评 本题主要考查圆的切线的判定定理的证明、弦切角的应用、三角形相似等基础知识,考查运化归与转化思想.属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
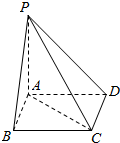 如图所示,四边形ABCD是正方形,PA⊥平面ABCD,且PA=AB.
如图所示,四边形ABCD是正方形,PA⊥平面ABCD,且PA=AB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?m∈R,函数f(x)在定义域上单调递增 | B. | ?m∈R,函数f(x)存在零点 | ||
| C. | ?m∈R,函数f(x)有最大值 | D. | ?m∈R,函数f(x)没有最小值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
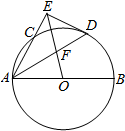 如图,AB是圆O的直径,AC是弦,∠BAC的平分线AD交圆O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.
如图,AB是圆O的直径,AC是弦,∠BAC的平分线AD交圆O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com