
【题目】(题文)在三棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() 且三棱锥
且三棱锥![]() 的每个顶点都在球
的每个顶点都在球![]() 的表面上,则球
的表面上,则球![]() 的表面积为 _______
的表面积为 _______
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() (
(![]() )的上顶点为
)的上顶点为![]() ,圆
,圆![]() 经过点
经过点![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 作直线
作直线![]() 的垂线
的垂线![]() 交圆
交圆![]() 于另一点
于另一点![]() .若△PQN的面积为3,求直线
.若△PQN的面积为3,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一直径为8米的半圆形空地,现计划种植甲、乙两种水果,已知单位面积种植甲水果的经济价值是种植乙水果经济价值的5倍,但种植甲水果需要有辅助光照.半圆周上的![]() 处恰有一可旋转光源满足甲水果生长的需要,该光源照射范围是
处恰有一可旋转光源满足甲水果生长的需要,该光源照射范围是![]() ,点
,点![]() 在直径
在直径![]() 上,且
上,且![]() .
.

(1)若![]() 米,求
米,求![]() 的长;
的长;
(2)设![]() , 求该空地产生最大经济价值时种植甲种水果的面积.
, 求该空地产生最大经济价值时种植甲种水果的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业引进现代化管理体制,生产效益明显提高.2018年全年总收入与2017年全年总收入相比增长了一倍,实现翻番.同时该企业的各项运营成本也随着收入的变化发生了相应变化.下图给出了该企业这两年不同运营成本占全年总收入的比例,下列说法正确的是( )
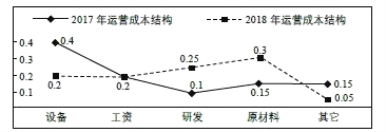
A.该企业2018年原材料费用是2017年工资金额与研发费用的和
B.该企业2018年研发费用是2017年工资金额、原材料费用、其它费用三项的和
C.该企业2018年其它费用是2017年工资金额的![]()
D.该企业2018年设备费用是2017年原材料的费用的两倍
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“伦敦眼”坐落在英国伦敦泰晤士河畔,是世界上首座观景摩天轮,又称“千禧之轮”,该摩天轮的半径为6(单位:![]() ),游客在乘坐舱
),游客在乘坐舱![]() 升到上半空鸟瞰伦敦建筑
升到上半空鸟瞰伦敦建筑![]() ,伦敦眼与建筑之间的距离
,伦敦眼与建筑之间的距离![]() 为12(单位:
为12(单位:![]() ),游客在乘坐舱
),游客在乘坐舱![]() 看建筑
看建筑![]() 的视角为
的视角为![]() .
.

(1)当乘坐舱![]() 在伦敦眼的最高点
在伦敦眼的最高点![]() 时,视角
时,视角![]() ,求建筑
,求建筑![]() 的高度;
的高度;
(2)当游客在乘坐舱![]() 看建筑
看建筑![]() 的视角
的视角![]() 为
为![]() 时,拍摄效果最好.若在伦敦眼上可以拍摄到效果最好的照片,求建筑
时,拍摄效果最好.若在伦敦眼上可以拍摄到效果最好的照片,求建筑![]() 的最低高度.
的最低高度.
(说明:为了便于计算,数据与实际距离有误差,伦敦眼的实际高度为![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面多边形![]() 中,四边形
中,四边形![]() 是边长为2的正方形,四边形
是边长为2的正方形,四边形![]() 为等腰梯形,
为等腰梯形,![]() 为
为![]() 的中点,
的中点,![]() ,现将梯形
,现将梯形![]() 沿
沿![]() 折叠,使平面
折叠,使平面![]() 平面
平面![]() .
.
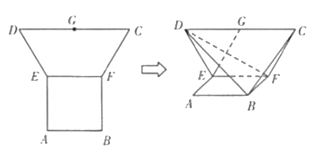
(1)求证:![]() 面
面![]() ;
;
(2)求![]() 与平面
与平面![]() 成角的正弦值.
成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年是中国改革开放的第40周年,为了充分认识新形势下改革开放的时代性,某地的民调机构随机选取了该地的100名市民进行调查,将他们的年龄分成6段:![]() ,并绘制了如图所示的频率分布直方图.
,并绘制了如图所示的频率分布直方图.
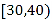
(1)现从年龄在![]() 内的人员中按分层抽样的方法抽取8人,再从这8人中随机抽取3人进行座谈,用
内的人员中按分层抽样的方法抽取8人,再从这8人中随机抽取3人进行座谈,用![]() 表示年龄在
表示年龄在![]() 内的人数,求
内的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)若用样本的频率代替概率,用随机抽样的方法从该地抽取20名市民进行调查,其中有![]() 名市民的年龄在
名市民的年龄在![]() 的概率为
的概率为![]() .当
.当![]() 最大时,求
最大时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com