
【题目】在平面直角坐标系xOy中,A(﹣2,0),B(2,0),P为不在x轴上的动点,直线PA,PB的斜率满足kPAkPB![]() .
.
(1)求动点P的轨迹Γ的方程;
(2)若M,N是轨迹Γ上两点,kMN=1,求△OMN面积的最大值.
【答案】(1)![]() (y≠0);(2)
(y≠0);(2)![]()
【解析】
(1)设P(x,y)为轨迹Γ上任意一点,根据kPAkPB![]() ,得到
,得到![]() ,化简即得解;
,化简即得解;
(2)设MN:y=x+b,联立得到韦达定理,利用弦长公式表示弦长|MN|,O到直线MN的距离,继而表示△OMN的面积,利用导数研究单调性,求最值即可.
(1)设P(x,y)为轨迹Γ上任意一点,则根据kPAkPB![]() .
.
即![]() ,
,
整理得动点P的轨迹Γ的方程为:![]() (y≠0);
(y≠0);
(2)设MN:y=x+b,联立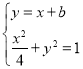 ,
,
整理得5x2+8bx+4b2﹣4=0,
△=5﹣b2>0,
设M(x1,y1),N(x2,y2),
则x1+x2![]() b,x1x2
b,x1x2![]() (b2﹣1),
(b2﹣1),
|MN|![]() |x1﹣x2|
|x1﹣x2|![]() ,
,
O到直线MN的距离d![]() ,
,
所以△OMN面积S![]() ,
,
设f(b)=5b2﹣b4,
则f′(b)=10b﹣4b3=0,
解得b=0或b=±![]() ,
,
又因为5﹣b2>0,
故b=0或b=±![]()
且S(0)=0,S(±![]() )
)![]() ,
,
故△OMN的面积S最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某工厂生产某款机器零件,因为要求精度比较高,所以需要对生产的一大批零件进行质量检测.首先由专家根据各种系数制定了质量指标值,从生产的大批零件中选取100件作为样本进行评估,根据评估结果作出如图所示的频率分布直方图.
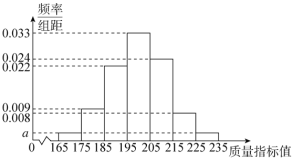
(1)(ⅰ)根据直方图求![]() 及这100个零件的样本平均数
及这100个零件的样本平均数![]() (同一组数据用该组数据区间的中点值表示);
(同一组数据用该组数据区间的中点值表示);
(ⅱ)以样本估计总体,经过专家研究,零件的质量指标值![]() ,试估计10000件零件质量指标值在
,试估计10000件零件质量指标值在![]() 内的件数;
内的件数;
(2)设每个零件利润为![]() 元,质量指标值为
元,质量指标值为![]() ,利润
,利润![]() 与质量指标值
与质量指标值![]() 之间满足函数关系
之间满足函数关系![]() .假设同组中的每个数据用该组区间的中点值代替,试估算该批零件的平均利润.(结果四舍五入,保留整数)
.假设同组中的每个数据用该组区间的中点值代替,试估算该批零件的平均利润.(结果四舍五入,保留整数)
参考数据:![]() ,则
,则![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列![]() 中,
中,![]() ,且
,且![]() ,
,![]() ,
,![]() 成等比数列.
成等比数列.
(1)求数列![]() 的通项公式;
的通项公式;
(2)记![]() 为数列
为数列![]() 的前
的前![]() 项和,是否存在正整数
项和,是否存在正整数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S—ABCD中,![]() 底面ABCD,底面ABCD是矩形,且
底面ABCD,底面ABCD是矩形,且![]() ,E是SA的中点.
,E是SA的中点.
(1)求证:平面BED![]() 平面SAB;
平面SAB;
(2)求平面BED与平面SBC所成二面角(锐角)的大小.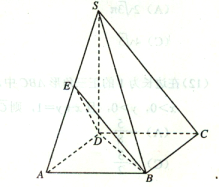
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两个班级均为 40 人,进行一门考试后,按学生考试成绩及格与不及格进行统计,甲班及格人数为 36 人,乙班及格人数为 24 人.
(1)根据以上数据建立一个2![]() 2的列联表;
2的列联表;
(2)试判断是否成绩与班级是否有关?
参考公式:![]() ;
;![]()
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 分别为
分别为![]() 的左顶点和上顶点,若
的左顶点和上顶点,若![]() 的中点的纵坐标为
的中点的纵坐标为![]() .
.![]() 分别为
分别为![]() 的左、右焦点.
的左、右焦点.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与
与![]() 交于
交于![]() 两点,
两点,![]() ,
,![]() 的重心分别为
的重心分别为![]() .若原点
.若原点![]() 在以
在以![]() 为直径的圆内,求实数
为直径的圆内,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某外国语学校举行的![]() (高中生数学建模大赛)中,参与大赛的女生与男生人数之比为
(高中生数学建模大赛)中,参与大赛的女生与男生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() ,分数在
,分数在![]() 以上(含
以上(含![]() )的同学获奖.按女生、男生用分层抽样的方法抽取
)的同学获奖.按女生、男生用分层抽样的方法抽取![]() 人的成绩作为样本,得到成绩的频率分布直方图如图所示.
人的成绩作为样本,得到成绩的频率分布直方图如图所示.
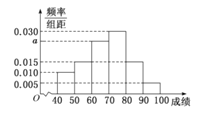
(Ⅰ)求![]() 的值,并计算所抽取样本的平均值
的值,并计算所抽取样本的平均值![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)填写下面的![]() 列联表,并判断在犯错误的概率不超过
列联表,并判断在犯错误的概率不超过![]() 的前提下能否认为“获奖与女生、男生有关”.
的前提下能否认为“获奖与女生、男生有关”.
女生 | 男生 | 总计 | |
获奖 |
| ||
不获奖 | |||
总计 |
| ||
附表及公式:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中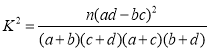 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,过动点
,过动点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,且
,且![]() .记动点
.记动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 交曲线
交曲线![]() 于不同的两点
于不同的两点![]() ,
,![]() .
.
①若![]() 为线段
为线段![]() 的中点,求直线
的中点,求直线![]() 的方程;
的方程;
②设![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,求
,求![]() 面积
面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com