
【题目】如图,已知椭圆 ![]() (a>b>0)的离心率为
(a>b>0)的离心率为 ![]() ,以该椭圆上的点和椭圆的左、右焦点F1 , F2为顶点的三角形的周长为
,以该椭圆上的点和椭圆的左、右焦点F1 , F2为顶点的三角形的周长为 ![]() .一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.
.一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D. 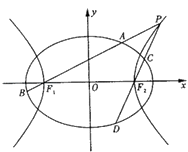
(1)求椭圆和双曲线的标准方程;
(2)设直线PF1、PF2的斜率分别为k1、k2 , 证明k1k2=1;
(3)探究 ![]() 是否是个定值,若是,求出这个定值;若不是,请说明理由.
是否是个定值,若是,求出这个定值;若不是,请说明理由.
【答案】
(1)解:设椭圆的半焦距为c,由题意知: ![]() ,2a+2c=4(
,2a+2c=4( ![]() +1)
+1)
解得a=2 ![]() ,c=2,
,c=2,
又a2=b2+c2,解得b=2.
故椭圆的标准方程为 ![]()
由题意设等轴双曲线的标准方程为 ![]() (m>0),
(m>0),
因为等轴双曲线的顶点是椭圆的焦点.
所以m=2,
因此双曲线的标准方程为 ![]()
(2)证明:设P(x0,y0),F1(﹣2,0),F2(2,0)
则k1= ![]() ,
, ![]() .
.
因为点P在双曲线x2﹣y2=4上,所以 ![]() .
.
因此 ![]() ,
,
故k1k2=1.
(3)解:设A(x1,y1),B(x2,y2),
由于PF1的方程为y=k1(x+2),将其代入椭圆方程得 ![]()
所以 ![]() ,
,
所以 ![]() =
= 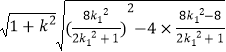 =
= ![]()
同理可得 ![]() .
.
则 ![]() ,
,
又k1k2=1,
所以 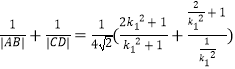 =
= ![]() .
.
故 ![]() 恒成立,即
恒成立,即 ![]() 是定值
是定值 ![]()
【解析】(1)由椭离心率为 ![]() ,以该椭圆上的点和椭圆的左、右焦点F1 , F2为顶点的三角形的周长为
,以该椭圆上的点和椭圆的左、右焦点F1 , F2为顶点的三角形的周长为 ![]() ,求出a,b,从而能求出椭圆的标准方程,设等轴双曲线的标准方程为
,求出a,b,从而能求出椭圆的标准方程,设等轴双曲线的标准方程为 ![]() ,由等轴双曲线的顶点是椭圆的焦点,求出m,从而能求出双曲线的标准方程.(2)设P(x0 , y0),F1(﹣2,0),F2(2,0),则k1=
,由等轴双曲线的顶点是椭圆的焦点,求出m,从而能求出双曲线的标准方程.(2)设P(x0 , y0),F1(﹣2,0),F2(2,0),则k1= ![]() ,
, ![]() ,由此能证明k1k2=1.(3)PF1的方程为y=k1(x+2),将其代入椭圆方程得
,由此能证明k1k2=1.(3)PF1的方程为y=k1(x+2),将其代入椭圆方程得 ![]() ,由此利用韦达定理、弦长公式,结合已知条件能推导出
,由此利用韦达定理、弦长公式,结合已知条件能推导出 ![]() 是定值.
是定值.


科目:高中数学 来源: 题型:
【题目】已知数列{bn}是首项b1=1,b4=10的等差数列,设bn+2=3 ![]() an(n∈n*).
an(n∈n*).
(1)求证:{an}是等比数列;
(2)记cn= ![]() ,求数列{cn}的前n项和Sn;
,求数列{cn}的前n项和Sn;
(3)记dn=(3n+1)Sn , 若对任意正整数n,不等式 ![]() +
+ ![]() +…+
+…+ ![]() >
> ![]() 恒成立,求整数m的最大值.
恒成立,求整数m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍.为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为( )
A.9
B.18
C.27
D.36
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子中装有4张卡片,每张卡片上写有1个数字,数字分别是1,2,3,4,现从盒子中随机抽取卡片.
(1)若一次从中随机抽取3张卡片,求3张卡片上数字之和大于或等于8的概率;
(2)若随机抽取1张卡片,放回后再随机抽取1张卡片,求两次抽取的卡片中至少一次抽到数字3的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店计划每天购进某商品若干件,商店每销售1件该商品可获利50元.若供大于求,剩余商品全部退回,则每件商品亏损10元;若供不应求,则从外部调剂,此时每件调剂商品可获利30元.
(Ⅰ)若商店一天购进该商品10件,求当天的利润y(单位:元)关于当天需求量n(单位:件,n∈N)的函数解析式;
(Ⅱ)商店记录了50天该商品的日需求量(单位:件),整理得下表:
日需求量n | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 10 | 15 | 10 | 5 |
①假设该店在这50天内每天购进10件该商品,求这50天的日利润(单位:元)的平均数;
②若该店一天购进10件该商品,记“当天的利润在区间![]() ”为事件A,求P(A)的估计值.
”为事件A,求P(A)的估计值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“奶茶妹妹”对某时间段的奶茶销售量及其价格进行调查,统计出售价x元和销售量y杯之间的一组数据如下表所示:
价格x | 5 | 5.5 | 6.5 | 7 |
销售量y | 12 | 10 | 6 | 4 |
通过分析,发现销售量y对奶茶的价格x具有线性相关关系.
(Ⅰ)求销售量y对奶茶的价格x的回归直线方程;
(Ⅱ)欲使销售量为13杯,则价格应定为多少?
注:在回归直线y= ![]() 中,
中, 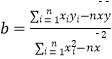 ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
. ![]() =146.5.
=146.5.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,a1=1,an+1=2an+1 (I)求证数列{an+1}是等比数列;
(II)设cn=n(an+1),求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为考察高中生的性别与是否喜欢数学课程之间的关系,在某城市的某校高中生中,从男生中随机抽取了70人,从女生中随机抽取了50人,男生中喜欢数学课程的占![]() ,女生中喜欢数学课程的占
,女生中喜欢数学课程的占![]() ,得到如下列联表.
,得到如下列联表.
喜欢数学课程 | 不喜欢数学课程 | 合计 | ||||||||
男生 | ||||||||||
女生 | ||||||||||
合计 | ||||||||||
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 | |||
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 | |||
(1)请将列联表补充完整;试判断能否有90%的把握认为喜欢数学课程与否与性别有关;
(2)从不喜欢数学课程的学生中采用分层抽样的方法,随机抽取6人,现从6人中随机抽取2人,若所选2名学生中的女生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:![]() ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com