
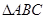 中,角A,B,C的对边分别是
中,角A,B,C的对边分别是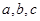 且满足
且满足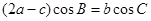
(1)求角B的大小;
(2)若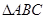 的面积为为
的面积为为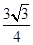 且
且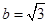 ,求
,求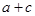 的值;
的值;
(1)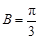 . ⑵a+c=
. ⑵a+c=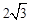 .
.
【解析】
试题分析:(1)又A+B+C=π,即C+B=π-A,
∴sin(C+B)=sin(π-A)=sinA,
将(2a-c)cosB=bcosC,利用正弦定理化简得:(2sinA-sinC)cosB=sinBcosC,
∴2sinAcosB=sinCcosB+sinBcosC=sin(C+B)=sinA,
在△ABC中,0<A<π,sinA>0,
∴cosB=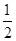 ,又0<B<π,则
,又0<B<π,则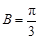 ;
;
(2)∵△ABC的面积为 ,sinB=sin
,sinB=sin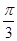 =
=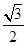 ,
,
∴S=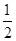 acsinB=
acsinB=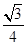 ac=
ac= ,
,
∴ac=3,又b=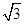 ,cosB=cos
,cosB=cos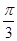 =
=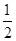 ,
,
∴由余弦定理b2=a2+c2-2accosB得:a2+c2-ac=(a+c)2-3ac=(a+c)2-9=3,
∴(a+c)2=12,
则a+c=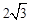 .
.
考点:考查主要考查正弦、余弦定理的应用,诱导公式,两角和与差的正弦函数公式,三角形的面积公式,以及特殊角的三角函数值。
点评:中档题,本题综合考查了正弦、余弦定理的应用,诱导公式,两角和与差的正弦函数公式,三角形的面积公式,以及特殊角的三角函数值。其中(2)将sinB及已知面积代入求出ac的值,利用余弦定理得到b2=a2+c2-2accosB,再利用完全平方公式整理后,按整体思想求出a+c的值。


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源:2011-2012学年江苏省苏北四市高三第三次模拟考试数学试卷(解析版) 题型:解答题
(本小题满分14分)
 中,角A,B,C的对边分别是
中,角A,B,C的对边分别是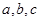 且满足
且满足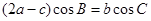
(1) 求角B的大小;
(2) 若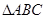 的面积为为
的面积为为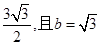 ,求
,求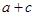 的值;
的值;
查看答案和解析>>
科目:高中数学 来源:2014届江苏省南京实验国际学校高一下学期期中考试数学试卷(解析版) 题型:解答题
在 中,角A,B,C的对边分别是a,b,c,已知
中,角A,B,C的对边分别是a,b,c,已知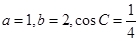
(1)求 的周长
(5分)
的周长
(5分)
(2)求值: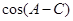 的值(5分)
的值(5分)
查看答案和解析>>
科目:高中数学 来源:2011-2012学年四川省绵阳市高三第二次月考理科数学试卷 题型:解答题
已知向量
 函数
函数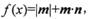 且最小正周期为
且最小正周期为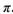 .
.
(I)求函数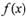 的最大值,并写出相应的X的取值集合;
的最大值,并写出相应的X的取值集合;
(II)在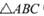 中,角A,B, C所对的边分别为a, b,c,且
中,角A,B, C所对的边分别为a, b,c,且 ,c=3,
,c=3,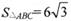 ,求b的值.
,求b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com