

思路分析:正方形的面积=|AB|2.因此,要用正方形的性质,把AB的直线方程求出来.进而求出弦长,问题得解.
解法一:设AB:y=x+b,代入抛物线方程得x2-x-b=0,
∴x1+x2=1,x1x2=-b.
|AB|=![]() ,而|AD|=
,而|AD|=![]() ,
,
∴![]() ,解得b=6或2.
,解得b=6或2.
∴正方形面积=|AB|2=2+8b=50或18.
解法二:设正方形ABCD的边长为d,
则直线AB是把CD向上平移![]() d而得,
d而得,
设方程为y=x-4+![]() d.
d.
由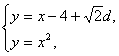
消去y得x2-x+4-![]() d=0.
d=0.
由韦达定理得x1+x2=1,x1x2=4-![]() d.
d.
∴|AB|=![]() |x1-x2|=
|x1-x2|=![]() ·
·![]() =
=![]() ·
·![]() .
.
又∵|AB|=d,∴d2=2(4![]() d-15).
d-15).
解得d=3![]() 或d=5
或d=5![]() .
.
∴正方形ABCD的面积是18或50.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 2 |
| A、18或25 | B、9或25 |
| C、18或50 | D、9或50 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 的双曲线:32y2-mx2=1的一个焦点,正方形ABCD的两个顶点A、B在拋物线E上,C,D两点在直线y=x-4上,则该正方形的面积是
的双曲线:32y2-mx2=1的一个焦点,正方形ABCD的两个顶点A、B在拋物线E上,C,D两点在直线y=x-4上,则该正方形的面积是查看答案和解析>>
科目:高中数学 来源:2011年四川省德阳市高考数学二模试卷(文科)(解析版) 题型:选择题
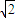 的双曲线:32y2-mx2=1的一个焦点,正方形ABCD的两个顶点A、B在拋物线E上,C,D两点在直线y=x-4上,则该正方形的面积是( )
的双曲线:32y2-mx2=1的一个焦点,正方形ABCD的两个顶点A、B在拋物线E上,C,D两点在直线y=x-4上,则该正方形的面积是( )查看答案和解析>>
科目:高中数学 来源:2011年四川省德阳市高考数学二模试卷(理科)(解析版) 题型:选择题
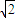 的双曲线:32y2-mx2=1的一个焦点,正方形ABCD的两个顶点A、B在拋物线E上,C,D两点在直线y=x-4上,则该正方形的面积是( )
的双曲线:32y2-mx2=1的一个焦点,正方形ABCD的两个顶点A、B在拋物线E上,C,D两点在直线y=x-4上,则该正方形的面积是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com