(本小题满分14分)
已知数

列
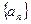
满足
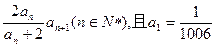
。
(Ⅰ)

求证:数列
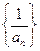
是等差数列,并求通项
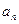
;
(Ⅱ)若
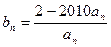
,且
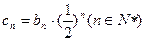
,求和
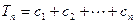
;
(Ⅲ)比较
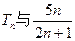
的大小,并予以证明。
解析:(Ⅰ)
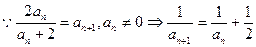
数列
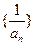
是首项为
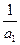
,公差为
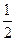
的等差数列,…………2分
故
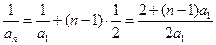
因为
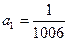
所以数列
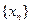
的通项公式为

……4分
(Ⅱ)将
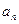
代入
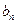
可求得
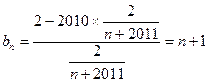
所以
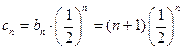
…………5分[
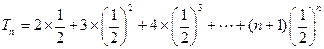
①
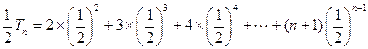
②…………7分
由①-②得
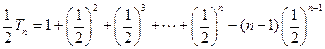
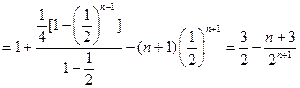

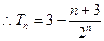
…………9分
(Ⅲ)

于是确定
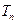
与
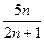
的大小关系等价于比较

与

的大小
由
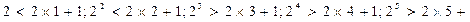
1,
可猜想当时,
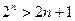
…………11分
证明如下:
证法1:(1)当
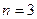
时,由上验算显

示成立,
(2)假设

时成立,即
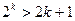
则
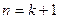
时
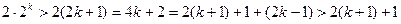
所以当
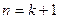
时猜想也成立
综合

可知,对一切
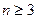
的正整数,都有
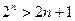
…………12分
证法2:当
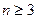
时
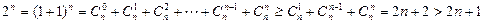
12分
综上所述,当

时,

当
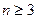
时,
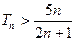
……14
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
.(本小题满分12分)数列

的前
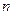
项和记为

,
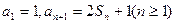
(1) 求

的通项公式;
(2) 等差数列

的各项为正,其前
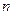
项和为
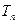
,且
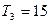
,
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
:数列
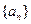
满足:
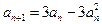
,
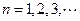
.
(Ⅰ)若数列
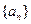
为常数列,求
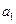
的值;
(Ⅱ)若
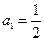
,求证:
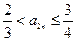
;(Ⅲ)在(Ⅱ)的条件下,求证:数列
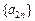
单调递减.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(10分)
设
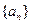
为等差数列,
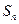
为数列
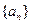
的前
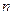
项和,已知
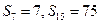
,
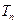
为数列
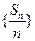
的前
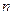
项和,求
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
等差数列
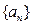
的前
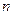
项和为
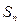
,且
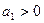
,若存在自然数
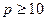
,使得
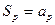
,则当
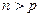
时,
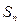
与
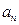
的大小关系是 ( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知数列
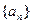
的通项公式为
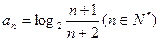
,设
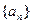
的前n项和为
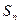
,则使
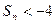
成立的自然数n( )
| A.有最大值31 | B.有最小值31 | C.有最小值15 | D.有最大值15 |
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
(理)在等比数列
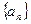
中,首项
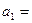
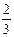
,
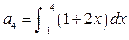
,则公比
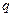
为
.
(文)等比数列
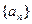
中,
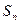
是其前
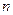
项和,
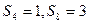
,则
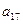
+
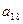
+
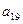
+
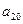
=
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
若数列
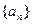
是正项数列,且
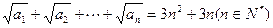
则
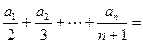
__________________.
查看答案和解析>>

 列
列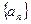 满足
满足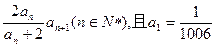 。
。 求证:数列
求证:数列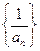 是等差数列,并求通项
是等差数列,并求通项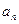 ;
;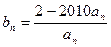 ,且
,且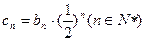 ,求和
,求和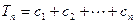 ;
;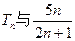 的大小,并予以证明。
的大小,并予以证明。 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案