
分析 (1)运用圆与圆的位置关系,|F1F2|=2$\sqrt{3}$和a,b,c的关系,计算即可得到b,进而得到椭圆C的方程;
(2)求得椭圆E的方程,①设P(x0,y0),$\frac{|OQ|}{|OP|}$=λ,求得Q的坐标,分别代入椭圆C,E的方程,化简整理,即可得到所求值;
②设A(x1,y1),B(x2,y2),将直线y=kx+m代入椭圆E的方程,运用韦达定理,三角形的面积公式,将直线y=kx+m代入椭圆C的方程,由判别式大于0,可得t的范围,结合二次函数的最值,又△ABQ的面积为3S,即可得到所求的最大值.
解答 解:(1)由题意可知,|PF1|+|PF2|=2a=4,可得a=2,
又|F1F2|=2$\sqrt{3}$,∴c=$\sqrt{3}$,
∵a2-c2=b2,
∴b=1,即有椭圆C的方程为$\frac{{x}^{2}}{4}$+y2=1;
(2)由(1)知椭圆E的方程为$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}$=1,
①设P(x0,y0),$\frac{|OQ|}{|OP|}$=λ,由题意可知,
Q(-λx0,-λy0),由于$\frac{{{x}_{0}}^{2}}{4}$+y02=1,
代入化简可得$\frac{{λ}^{2}}{4}$($\frac{{{x}_{0}}^{2}}{4}$+y02)=1,
所以λ=2,即$\frac{|OQ|}{|OP|}$=2;
②设A(x1,y1),B(x2,y2),将直线y=kx+m代入椭圆E的方程,可得
(1+4k2)x2+8kmx+4m2-16=0,由△>0,可得m2<4+16k2,③
则有x1+x2=-$\frac{8km}{1+4{k}^{2}}$,x1x2=$\frac{4{m}^{2}-16}{1+4{k}^{2}}$,所以|x1-x2|=$\frac{\root{4}{16{k}^{2}+4-{m}^{2}}}{1+4{k}^{2}}$,
由直线y=kx+m与y轴交于(0,m),
则△AOB的面积为S=$\frac{1}{2}$|m|•|x1-x2|=$\frac{1}{2}$|m|•$\frac{\root{4}{16{k}^{2}+4-{m}^{2}}}{1+4{k}^{2}}$
设$\frac{{m}^{2}}{1+4{k}^{2}}$=t,则S=2$\sqrt{t(4-t)}$,
将直线y=kx+m代入椭圆C的方程,可得(1+4k2)x2+8kmx+4m2-4=0,
由△′≥0可得m2≤1+4k2,④
由③④可得0<t≤1,则S=2$\sqrt{-(t-2)^{2}+4}$在(0,1]递增,即有t=1取得最大值,
即有S≤2$\sqrt{3}$,即m2=1+4k2,取得最大值2$\sqrt{3}$,
由①知,△ABQ的面积为3S,
即△ABQ面积的最大值为6$\sqrt{3}$.
点评 本题考查椭圆的方程和性质,主要考查直线方程和椭圆方程联立,运用韦达定理,同时考查三角形的面积公式和二次函数的最值,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1.14a | B. | 1.15a | C. | 10a(1.16-1) | D. | 10a(1.15-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | [0,1) | C. | (0,1] | D. | [0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 年份x | 2004 | 2005 | 2006 | 2007 |
| 恩格尔系数y(%) | 47 | 45.5 | 43.5 | 41 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 14 | B. | 15 | C. | 16 | D. | 17 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2或0 | B. | 0或1 | C. | ±1 | D. | ±2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
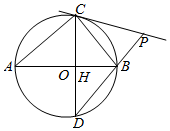 如图,△ABC内接于⊙O,AB为其直径,CH⊥AB于H延长后交⊙O于D,连接DB并延长交过C点的直线于P,且CB平分∠DCP.
如图,△ABC内接于⊙O,AB为其直径,CH⊥AB于H延长后交⊙O于D,连接DB并延长交过C点的直线于P,且CB平分∠DCP.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com