练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知在正四棱锥P-ABCD中，侧棱与底面成角为60°，且侧面积为，则四棱锥P-ABCD的内切球的表面积为（ ）

    A.B.

    C.D.

    【答案】B

    【解析】

    取AD的中点E，作面ABCD，垂足为O，过PO及棱AD、BC的中点E、F作正四棱锥P-ABCD的轴截面PEF，设，四棱锥内切球的半径为r，利用对称性求出，即得四棱锥P-ABCD的内切球的表面积.

    如图，取AD的中点E，作面ABCD，垂足为O，过PO及棱AD、BC的中点E、F作正四棱锥P-ABCD的轴截面PEF，

    设，四棱锥内切球的半径为r，则，

    则，，，，

    则，得.

    由正四棱锥与球的对称性知该正四棱锥的内切球半径与内切圆的半径相等，

    故，

    解得，所以

    即正四棱锥P-ABCD的内切球的表面积为.

    故选：B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】为迎接2022年冬奥会，北京市组织中学生开展冰雪运动的培训活动，并在培训结束后对学生进行了考核．记表示学生的考核成绩，并规定为考核优秀．为了了解本次培训活动的效果，在参加培训的学生中随机抽取了30名学生的考核成绩，并作成如下茎叶图：

    （Ⅰ）从参加培训的学生中随机选取1人，请根据图中数据，估计这名学生考核优秀的概率；

    （Ⅱ）从图中考核成绩满足的学生中任取2人，求至少有一人考核优秀的概率；

    （Ⅲ）记表示学生的考核成绩在区间的概率，根据以往培训数据，规定当时培训有效．请根据图中数据，判断此次中学生冰雪培训活动是否有效，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】研究机构对某校学生往返校时间的统计资料表明：该校学生居住地到学校的距离（单位：千米）和学生花费在上学路上的时间（单位：分钟）有如下的统计资料：

    到学校的距离（千米）

    1.8

    2.6

    3.1

    4.3

    5.5

    6.1

    花费的时间（分钟）

    17.8

    19.6

    27.5

    31.3

    36.0

    43.2

    如果统计资料表明与有线性相关关系，试求：

    （1）判断与是否有很强的线性相关性？

    （相关系数的绝对值大于0.75时，认为两个变量有很强的线性相关性，精确到0.01）

    （2）求线性回归方程（精确到0.01）；

    （3）将分钟的时间数据称为美丽数据，现从这6个时间数据中任取2个，求抽取的2个数据全部为美丽数据的概率.

    参考数据：，，，，

    ，

    参考公式：，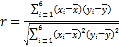

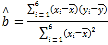
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】菜市房管局为了了解该市市民2018年1月至2019年1月期间购买二手房情况，首先随机抽样其中200名购房者，并对其购房面积（单位：平方米，）进行了一次调查统计，制成了如图1所示的频率分布南方匿，接着调查了该市2018年1月﹣2019年1月期间当月在售二手房均价（单位：万元/平方米），制成了如图2所示的散点图（图中月份代码1﹣13分别对应2018年1月至2019年1月）．

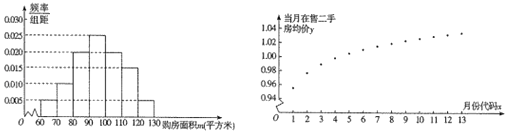
    （1）试估计该市市民的平均购房面积．

    （2）现采用分层抽样的方法从购房耐积位于的40位市民中随机取4人，再从这4人中随机抽取2人，求这2人的购房面积恰好有一人在的概率．

    （3）根据散点图选择和两个模型进行拟合，经过数据处理得到两个回归方程，分别为和，并得到一些统计量的值，如表所示：

    请利用相关指数判断哪个模型的拟合效果更好，并用拟合效果更好的模型预测2019年6月份的二手房购房均价（精确到）．

    参考数据：，，，，,,,．参考公式：相关指数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】[选修4—4：坐标系与参数方程]

    在平面直角坐标系中，曲线的参数方程为（为参数，），以坐标原点为极点，轴的非负半轴为极轴，建立极坐标系，直线的极坐标方程为.

    （1）设是曲线上的一个动眯，当时，求点到直线的距离的最小值；

    （2）若曲线上所有的点都在直线的右下方，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （1）当时，关于的不等式恒成立，求实数的取值范围；

    （2）求证：对于任意的正整数，不等式恒成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）求的单调区间；

    （2）若在上成立，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，椭圆C：(a＞b＞0)经过点(0，)，点F是椭圆的右焦点，点F到左顶点的距离和到右准线的距离相等．过点F的直线交椭圆于M，N两点．

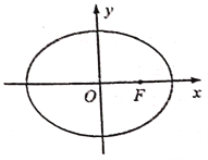
    （1）求椭圆C的标准方程；

    （2）当MF＝2FN时，求直线的方程；

    （3）若直线上存在点P满足PM·PN＝PF2，且点P在椭圆外，证明：点P在定直线上．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知.

    （1）求的单调区间；

    （2）当时，求证：对于，恒成立；

    （3）若存在，使得当时，恒有成立，试求的取值范围.

    查看答案和解析>>

    同步练习册答案