Question

20．已知F₁、F₂是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、焦点，过F₂作垂直于x轴的直线交双曲线于点P，当∠PF₁F₂=45°时，求双曲线的渐近线方程．

Answer 1

分析 先将x=c带人双曲线方程，求出y²=$\frac{{b}^{4}}{{a}^{2}}$，而根据∠F₁PF₂=45°知道△PF₁F₂为等腰直角三角形，从而得到4c²=$\frac{{b}^{4}}{{a}^{2}}$，通过该式即可求得该双曲线的渐近线方程．

解答 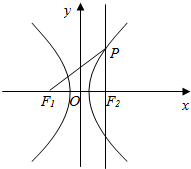解：如图，
由x=c与$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1联立得，y²=$\frac{{b}^{4}}{{a}^{2}}$；
∵∠F₁PF₂=45°；
∴|F₁F₂|=|PF₂|；
∴4c²=$\frac{{b}^{4}}{{a}^{2}}$；
∴4（a²+b²）a²=b⁴；
∴4a⁴+4a²b²-b⁴=0；
∴（$\frac{b}{a}$）⁴-4（$\frac{b}{a}$）²-4=0，
∴$\frac{b}{a}$=$\sqrt{2+2\sqrt{2}}$．
∴此双曲线的渐近线方程为y=±$\sqrt{2+2\sqrt{2}}$x．

点评 考查双曲线的标准方程，双曲线的焦点及焦距，一元二次方程的求根公式，双曲线的渐近线方程的概念及求法．