
【题目】已知动点P(x,y)满足|x﹣1|+|y﹣a|=1,O为坐标原点,若![]() 的最大值的取值范围为
的最大值的取值范围为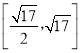 ,则实数a的取值范围是_____.
,则实数a的取值范围是_____.
【答案】![]() .
.
【解析】
先考虑|x﹣1|+|y﹣a|=1的图象,图象是(0,a),(1,a﹣1),(1,a+1),(2,a)为端点的正方形,那么和O最远的应该是最远的两个端点之一,再对a进行分类讨论,如果a>0就是(1,a+1)或(2,a);如果a<0就是(1,a﹣1)或(2,a).再分类写出|![]() |平方的最大值.最后利用分段函数的图象,再读出|
|平方的最大值.最后利用分段函数的图象,再读出|![]() |2取值范围为[
|2取值范围为[![]() ,17]时,a取值范围.
,17]时,a取值范围.
考虑|x﹣1|+|y﹣a|=1的图象,如图,

x必然是在0到2之间
x取到0或2那么y只能取a
x在两者之间y可以取两个值
x取到1则y可以取a+1或a﹣1,
图象是(0,a),(1,a﹣1),(1,a+1),(2,a)为端点的正方形,那么和O最远的应该是最远的两个端点之一,
如果a>0就是(1,a+1)或(2,a)
如果a<0就是(1,a﹣1)或(2,a)
这样一来,|![]() |平方的最大值就是:
|平方的最大值就是:
当a>0,(a+1)2+1或 a2+4
当a<0,(a﹣1)2+1或 a2+4
比较它们的大小:
当a≥1时,(a+1)2+1![]() ,则(a+1)2+1更大;
,则(a+1)2+1更大;
当0<a<1时,(a+1)2+1-(a2+4)![]() 且当﹣1<a<0时,
且当﹣1<a<0时,![]() ,则当﹣1<a<1时,a2+4更大;
,则当﹣1<a<1时,a2+4更大;
当a≤﹣1时,![]() ,则(a-1)2+1更大;
,则(a-1)2+1更大;
作以上函数图象,再读出|![]() |2取值范围为[
|2取值范围为[![]() ,17],即有
,17],即有

 或
或![]()
所以a取值范围是![]() .
.
故答案为:![]() .
.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】蜂巢是由工蜂分泌蜂蜡建成的.从正面看,蜂巢口是由许多正六边形的中空柱状体连接而成,中空柱状体的底部是由三个全等的菱形面构成.如图,在正六棱柱![]() 的三个顶点
的三个顶点![]() 处分别用平面
处分别用平面![]() ,平面
,平面![]() ,平面
,平面![]() 截掉三个相等的三棱锥
截掉三个相等的三棱锥![]() ,
,![]() ,
,![]() ,平面
,平面![]() ,平面
,平面![]() ,平面
,平面![]() 交于点
交于点![]() ,就形成了蜂巢的结构,如下图(4)所示,
,就形成了蜂巢的结构,如下图(4)所示,
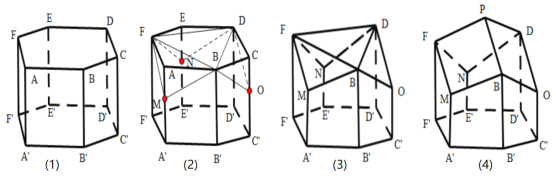
瑞士数学家克尼格利用微积分的方法证明了蜂巢的这种结构是在相同容积下所用材料最省的,英国数学家麦克劳林通过计算得到菱形的一个内角为![]() ,即
,即![]() .以下三个结论①
.以下三个结论①![]() ;②
;② ![]()
![]()
![]() ;③
;③![]() 四点共面,正确命题的个数为______个;若
四点共面,正确命题的个数为______个;若![]() ,
,![]() ,
,![]() ,则此蜂巢的表面积为_______.
,则此蜂巢的表面积为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P-ABCD的底面是正方形,![]() 底面ABCD,
底面ABCD,![]() ,E是侧棱的中点.
,E是侧棱的中点.
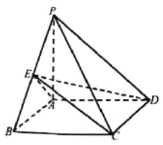
(1)求异面直线AE与PD所成的角;
(2)求点B到平面ECD的距离
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,侧面PAD是等边三角形,且平面
中,侧面PAD是等边三角形,且平面![]() 平面ABCD,
平面ABCD,![]() ,
,![]() .
.
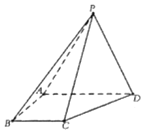
(1)AD上是否存在一点M,使得平面![]() 平面ABCD;若存在,请证明,若不存在,请说明理由;
平面ABCD;若存在,请证明,若不存在,请说明理由;
(2)若![]() 的面积为
的面积为![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
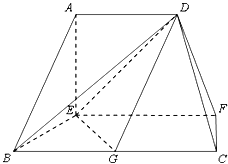
(Ⅰ)求证:AB∥平面DEG;
(Ⅱ)求证:BD⊥EG;
(Ⅲ)求多面体ADBEG的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
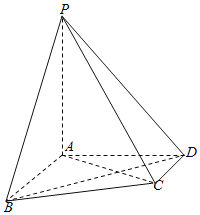
(1)证明:![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)设Q为线段PD上的点,且直线AQ和平面PAC所成角的正弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】生男生女都一样,女儿也是传后人.由于某些地区仍然存在封建传统思想,头胎的男女情况可能会影响生二孩的意愿,现随机抽取某地200户家庭进行调查统计.这200户家庭中,头胎为女孩的频率为0.5,生二孩的频率为0.525,其中头胎生女孩且生二孩的家庭数为60.
(1)完成下列![]() 列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
生二孩 | 不生二孩 | 合计 | |
头胎为女孩 | 60 | ||
头胎为男孩 | |||
合计 | 200 |
(2)在抽取的200户家庭的样本中,按照分层抽样的方法在生二孩的家庭中抽取了7户,进一步了解情况,在抽取的7户中再随机抽取4户,求抽到的头胎是女孩的家庭户数![]() 的分布列及数学期望.
的分布列及数学期望.
附:
| 0.15 | 0.05 | 0.01 | 0.001 |
| 2.072 | 3.841 | 6.635 | 10.828 |
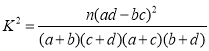 (其中
(其中![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四边形![]() 是边长为5的菱形,对角线
是边长为5的菱形,对角线![]() (如图1),现以
(如图1),现以![]() 为折痕将菱形折起,使点
为折痕将菱形折起,使点![]() 达到点
达到点![]() 的位置.棱
的位置.棱![]() ,
,![]() 的中点分为
的中点分为![]() ,
,![]() ,且四面体
,且四面体![]() 的外接球球心落在四面体内部(如图2),则线段
的外接球球心落在四面体内部(如图2),则线段![]() 长度的取值范围为( )
长度的取值范围为( )
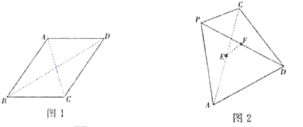
A.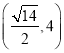 B.
B.![]() C.
C.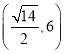 D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班级有60名学生,学号分别为1~60,其中男生35人,女生25人.为了了解学生的体质情况,甲、乙两人对全班最近一次体育测试的成绩分别进行了随机抽样.其中一人用的是系统抽样,另一人用的是分层抽样,他们得到各12人的样本数据如下所示,并规定体育成绩大于或等于80人为优秀.
甲抽取的样本数据:
学号 | 4 | 9 | 14 | 19 | 24 | 29 | 34 | 39 | 44 | 49 | 54 | 59 |
性别 | 男 | 女 | 男 | 男 | 女 | 男 | 女 | 男 | 女 | 女 | 男 | 男 |
体育成绩 | 90 | 80 | 75 | 80 | 83 | 85 | 75 | 80 | 70 | 80 | 83 | 70 |
女抽取的样本数据:
学号 | 1 | 8 | 10 | 20 | 23 | 28 | 33 | 35 | 43 | 48 | 52 | 57 |
性别 | 男 | 男 | 男 | 男 | 男 | 男 | 男 | 女 | 女 | 女 | 女 | 女 |
体育成绩 | 95 | 85 | 85 | 80 | 70 | 80 | 80 | 65 | 70 | 60 | 70 | 80 |
(Ⅰ)在乙抽取的样本中任取4人,记这4人中体育成绩优秀的学生人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)请你根据乙抽取的样本数据,判断是否有95%的把握认为体育成绩是否为优秀和性别有关;
(Ⅲ)判断甲、乙各用的何种抽样方法,并根据(Ⅱ)的结论判断哪种抽样方法更优,说明理由.
附: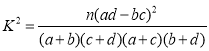
| 0.15 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com