
【题目】在棱长为2的正方体![]() 中,设
中,设![]() 是棱
是棱![]() 的中点.
的中点.
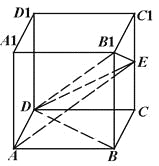
(1)求证:![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
试题本题考查了空间中的垂直与平行的判断与性质的应用问题,也考查了求几何体的体积的问题,(1)通过证明![]() 平面
平面![]() ,得出
,得出![]() ;(2)通过
;(2)通过![]() 的中位线证明线线平行,再证明线面平行;(3)点
的中位线证明线线平行,再证明线面平行;(3)点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,利用等积法求出三棱锥
的距离,利用等积法求出三棱锥![]() 的体积.
的体积.
试题解析:解:(1)【证明】连接BD,AE.因四边形ABCD为正方形,故![]() ,
,
因![]() 底面ABCD,
底面ABCD,![]() 面ABCD,故
面ABCD,故![]() ,又
,又![]() ,
,
故![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,故
,故![]() .
.
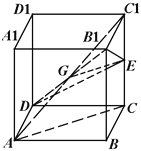
(2)连接![]() ,设
,设![]() ,连接
,连接![]() ,
,
则![]() 为
为![]() 中点,而
中点,而![]() 为
为![]() 的中点,故
的中点,故![]() 为三角形
为三角形![]() 的中位线,
的中位线,
![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() .
.
(3)由(2)知,点A到平面![]() 的距离等于C到平面
的距离等于C到平面![]() 的距离,
的距离,
故三棱锥![]() 的体积
的体积![]() ,
,
而![]() ,
,
三棱锥![]() 的体积为
的体积为![]() .…12分.
.…12分.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:
【题目】 设函数f(x)=(x-1)2+bln x,其中b为常数.
(1)当b>![]() 时,判断函数f(x)在定义域上的单调性;
时,判断函数f(x)在定义域上的单调性;
(2)若函数f(x)有极值点,求b的取值范围及f(x)的极值点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲,乙两台机床同时生产一种零件,其质量按测试指标划分:指标大于或等于100为优品,大于等于90且小于100为合格品,小于90为次品,现随机抽取这两台车床生产的零件各100件进行检测,检测结果统计如下:
测试指标 | [85,90) | [90,95) | [95,100) | [100,105) | [105,110) |
机床甲 | 8 | 12 | 40 | 32 | 8 |
机床乙 | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计甲机床、乙机床生产的零件为优品的概率;
(2)甲机床生产一件零件,若是优品可盈利160元,合格品可盈利100元,次品则亏损20元;假设甲机床某天生产50件零件,请估计甲机床该天的日利润(单位:元);
(3)从甲、乙机床生产的零件指标在[90,95)内的零件中,采用分层抽样的方法抽取5件,从这5件中任选2件进行质量分析,求这2件都是乙机床生产的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若曲线![]() 在
在![]() 处的切线的方程为
处的切线的方程为![]() ,求实数
,求实数![]() 的值;
的值;
(2)设![]() ,若对任意两个不等的正数
,若对任意两个不等的正数![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且a+b+c=8.
(1)若a=2,b=![]() ,求cosC的值;
,求cosC的值;
(2)若sinAcos2![]() +sinB·cos2
+sinB·cos2![]() =2sinC,且△ABC的面积S=
=2sinC,且△ABC的面积S=![]() sinC,求a和b的值.
sinC,求a和b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用二分法求函数![]() 的一个正零点的近似值(精确度为0.1)时,依次计算得到如下数据:f(1)=–2,f(1.5)=0.625,f(1.25)≈–0.984,f(1.375)≈–0.260,关于下一步的说法正确的是( )
的一个正零点的近似值(精确度为0.1)时,依次计算得到如下数据:f(1)=–2,f(1.5)=0.625,f(1.25)≈–0.984,f(1.375)≈–0.260,关于下一步的说法正确的是( )
A. 已经达到精确度的要求,可以取1.4作为近似值
B. 已经达到精确度的要求,可以取1.375作为近似值
C. 没有达到精确度的要求,应该接着计算f(1.4375)
D. 没有达到精确度的要求,应该接着计算f(1.3125)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化工厂一种溶液的成品,生产过程的最后工序是过滤溶液中的杂质,过滤初期溶液含杂质为2%,每经过一次过滤均可使溶液杂质含量减少![]() ,记过滤次数为x(
,记过滤次数为x(![]() )时溶液杂质含量为y.
)时溶液杂质含量为y.
(1)写出y与x的函数关系式;
(2)按市场要求,出厂成品杂质含量不能超过0.1%,问至少经过几次过滤才能使产品达到市场要求?(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)
已知![]() ,
, ![]() 为椭圆
为椭圆![]() 的左、右顶点,
的左、右顶点, ![]() 为其右焦点,
为其右焦点, ![]() 是椭圆
是椭圆![]() 上异于
上异于![]() ,
, ![]() 的动点,且
的动点,且![]() 面积的最大值为
面积的最大值为![]() .
.
(Ⅰ)求椭圆![]() 的方程及离心率;
的方程及离心率;
(Ⅱ)直线![]() 与椭圆在点
与椭圆在点![]() 处的切线交于点
处的切线交于点![]() ,当直线
,当直线![]() 绕点
绕点![]() 转动时,试判断以
转动时,试判断以![]()
为直径的圆与直线![]() 的位置关系,并加以证明.
的位置关系,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() (a>b>0)的离心率
(a>b>0)的离心率![]() ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为![]() .
.

(1)求椭圆的方程.
(2)已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com