
【题目】已知函数![]() .
.
(1)曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,
,![]() 时,
时,![]() ,都有
,都有![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)对f(x)求导后利用![]() -1,
-1,![]() 直接求解即可.
直接求解即可.
(2)先判断若![]() ,
,![]() 时,f(x)在区间
时,f(x)在区间![]() 上是减函数,利用单调性及
上是减函数,利用单调性及![]() 的大小去绝对值,得到
的大小去绝对值,得到![]() ,构造函数
,构造函数![]() 在x∈
在x∈![]() 时是增函数.可得
时是增函数.可得![]() ,即
,即![]() 在x∈
在x∈![]() 时恒成立.再构造g(x)=
时恒成立.再构造g(x)=![]() 利用导数分析其最值,即可得出实数a的取值范围.
利用导数分析其最值,即可得出实数a的取值范围.
(1)∵![]() =
=![]() ,∴
,∴![]() -2b=-1,
-2b=-1,![]() ,
,
∴b=![]() ,a=1.
,a=1.
(2)若![]() ,
,![]() 时,
时,![]() ,在x
,在x![]() 上
上![]() 恒成立,
恒成立,
∴f(x)在区间![]() 上是减函数.
上是减函数.
不妨设1<x1<x2<e,则![]() ,
,
则![]() 等价于
等价于![]() .
.
即![]() ,
,
即函数![]() 在x∈
在x∈![]() 时是增函数.
时是增函数.
∴![]() ,即
,即![]() 在x∈
在x∈![]() 时恒成立.令g(x)=
时恒成立.令g(x)=![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() =
=![]() -
-![]() =
=![]() <0在x∈
<0在x∈![]() 时恒成立,
时恒成立,
∴![]() 在x∈
在x∈![]() 时是减函数,且x=e时,y=
时是减函数,且x=e时,y=![]() >0,∴y>0在x∈
>0,∴y>0在x∈![]() 时恒成立,即
时恒成立,即![]() 在x∈
在x∈![]() 时恒成立, ∴ g(x) 在x∈
时恒成立, ∴ g(x) 在x∈![]() 时是增函数,∴g(x)<g(e)=e-3
时是增函数,∴g(x)<g(e)=e-3
∴![]() .
.
所以,实数a的取值范围是![]() .
.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:
【题目】“中国人均读书4.3本(包括网络文学和教科书),比韩国的11本、法国的20本、日本的40本、犹太人的64本少得多,是世界上人均读书最少的国家.”这个论断被各种媒体反复引用,出现这样的统计结果无疑是令人尴尬的,而且和其他国家相比,我国国民的阅读量如此之低,也和我国是传统的文明古国、礼仪之邦的地位不相符.某小区为了提高小区内人员的读书兴趣,特举办读书活动,准备进一定量的书籍丰富小区图书站,由于不同年龄段需看不同类型的书籍,为了合理配备资源,现对小区内看书人员进行年龄调查,随机抽取了一天40名读书者进行调查,将他们的年龄分成6段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 后得到如图所示的频率分布直方图.
后得到如图所示的频率分布直方图.

问:
(1)估计在40名读书者中年龄分布在![]() 的人数;
的人数;
(2)求40名读书者年龄的平均数和中位数;
(3)若从年龄在![]() 的读书者中任取2名,求这两名读书者年龄在
的读书者中任取2名,求这两名读书者年龄在![]() 的人数
的人数![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】①一个命题的逆命题为真,它的否命题也一定为真;
②在![]() 中,“
中,“![]() ”是“
”是“![]() 三个角成等差数列”的充要条件.
三个角成等差数列”的充要条件.
③![]() 是
是![]() 的充要条件;
的充要条件;
④命题“不等式x2+x-6>0的解为x<-3或x>2”的逆否命题是“若-3≤x≤2,则x2+x-6≤0”
以上说法中,判断错误的有___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,然后纵坐标不变,横坐标变为原来的
个单位,然后纵坐标不变,横坐标变为原来的![]() 倍,得到
倍,得到![]() 的图象,下面四个结论正确的是( )
的图象,下面四个结论正确的是( )
A. 函数![]() 在区间
在区间![]() 上为增函数
上为增函数
B. 将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后得到的图象关于原点对称
个单位后得到的图象关于原点对称
C. 点![]() 是函数
是函数![]() 图象的一个对称中心
图象的一个对称中心
D. 函数![]() 在
在![]() 上的最大值为
上的最大值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形,![]() ,
,![]() 是等边三角形,
是等边三角形,![]() 为
为![]() 的中点,
的中点,![]() .
.

(1)求证:![]() ;
;
(2)若![]() 在线段
在线段![]() 上,且
上,且![]() ,能否在棱
,能否在棱![]() 上找到一点
上找到一点![]() ,使平面
,使平面![]() 平面
平面![]() ?若存在,求四面体
?若存在,求四面体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() .
.
(1)若![]() ,且
,且![]() 是实系数一元二次方程
是实系数一元二次方程![]() 的一根,求
的一根,求![]() 和
和![]() 的值;
的值;
(2)若![]() 是纯虚数,已知
是纯虚数,已知![]() 时,
时,![]() 取得最大值,求
取得最大值,求![]() ;
;
(3)肖同学和谢同学同时独立地解答第(2)小题,己知两人能正确解答该题的概率分别是0.8和0.9,求该题能被正确解答的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学中有许多形状优美、寓意美好的曲线,曲线C:![]() 就是其中之一(如图).给出下列三个结论:
就是其中之一(如图).给出下列三个结论:

①曲线C恰好经过6个整点(即横、纵坐标均为整数的点);
②曲线C上任意一点到原点的距离都不超过![]() ;
;
③曲线C所围成的“心形”区域的面积小于3.
其中,所有正确结论的序号是
A. ①B. ②C. ①②D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年11月15日,我市召开全市创建全国文明城市动员大会,会议向全市人民发出动员令,吹响了集结号.为了了解哪些人更关注此活动,某机构随机抽取了年龄在15~75岁之间的100人进行调查,并按年龄绘制的频率分布直方图如图所示,其分组区间为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .把年龄落在
.把年龄落在![]() 和
和![]() 内的人分别称为“青少年人”和“中老年人”,经统计“青少年人”与“中老年人”的人数之比为
内的人分别称为“青少年人”和“中老年人”,经统计“青少年人”与“中老年人”的人数之比为![]() .
.

(1)求图中![]() 的值,若以每个小区间的中点值代替该区间的平均值,估计这100人年龄的平均值
的值,若以每个小区间的中点值代替该区间的平均值,估计这100人年龄的平均值![]() ;
;
(2)若“青少年人”中有15人关注此活动,根据已知条件完成题中的![]() 列联表,根据此统计结果,问能否有
列联表,根据此统计结果,问能否有![]() 的把握认为“中老年人”比“青少年人”更加关注此活动?
的把握认为“中老年人”比“青少年人”更加关注此活动?
关注 | 不关注 | 合计 | |
青少年人 | 15 | ||
中老年人 | |||
合计 | 50 | 50 | 100 |
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
附参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正四面体![]() 的顶点
的顶点![]() 、
、![]() 、
、![]() 分别在两两垂直的三条射线
分别在两两垂直的三条射线![]() ,
, ![]() ,
, ![]() 上,则在下列命题中,错误的是( )
上,则在下列命题中,错误的是( )
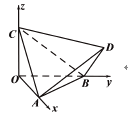
A. ![]() 是正三棱锥
是正三棱锥
B. 直线![]() 与平面
与平面![]() 相交
相交
C. 直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]()
D. 异面直线![]() 和
和![]() 所成角是
所成角是![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com