
【题目】直三棱柱![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 的中点,
的中点,![]() ,
,![]() 为棱
为棱![]() 上的点.
上的点.
(1)证明:![]() ;
;
(2)是否存在一点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() ?若存在,说明点
?若存在,说明点![]() 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.

【答案】(1)略 (2)![]() 为
为![]() 的中点
的中点
【解析】试题分析:对于问题(1)可以先证明![]() 两两垂直,然后再建立空间直角坐标系用向量法进行证明;对于问题(2)可在(1)中建立的坐标系下,分别求出平面
两两垂直,然后再建立空间直角坐标系用向量法进行证明;对于问题(2)可在(1)中建立的坐标系下,分别求出平面![]() 与平面
与平面![]() 的法向量,再根据二面角的余弦公式,即可确定是否存在一点
的法向量,再根据二面角的余弦公式,即可确定是否存在一点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.
试题解析:(1)证明:因为![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() 面
面![]() ,
,
又因为![]() 面
面![]() ,
,
所以![]() ,
,
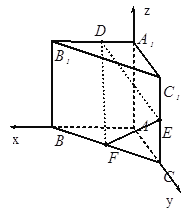
以![]() 为原点建立如图所示的空间直角坐标系
为原点建立如图所示的空间直角坐标系![]() ,则有
,则有
![]()
设![]() 且
且![]() ,即
,即![]() ,则
,则
![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]()
(2)结论:存在一点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]()
理由如下:
由题可知面![]() 的法向量
的法向量![]()
设面![]() 的法向量为
的法向量为![]() ,则
,则
因为![]() ,
,
所以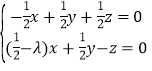 ,即
,即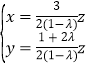 ,
,
令![]() ,则
,则![]()
因为平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() ,
,
所以![]() ,即
,即![]() ,
,
解得![]() 或
或![]() (舍),所以当
(舍),所以当![]() 为
为![]() 中点时满足要求
中点时满足要求


科目:高中数学 来源: 题型:
【题目】函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,周期是
,周期是![]() .
.
(1)求函数解析式,并写出函数图象的对称轴方程和对称中心;
(2)已知点![]() ,点
,点![]() 是该函数图象上一点,点
是该函数图象上一点,点![]() 是
是![]() 的中点,当
的中点,当![]() ,
, ![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学在用120分钟做150分的数学试卷(分为卷Ⅰ和卷Ⅱ两部分)时,卷Ⅰ和卷Ⅱ所得分数分别为P(单位:分)和Q(单位:分),在每部分做了20分钟的条件下发现它们与投入时间m(单位:分钟)的关系有经验公式,![]() .
.
(1)试建立数学总成绩y(单位:分)与对卷Ⅱ投入时间x(单位:分钟)的函数关系式,并指明函数定义域;
(2)如何计划使用时间,才能使得所得分数最高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知矩形![]() 的长为2,宽为1,
的长为2,宽为1, ![]() ,
, ![]() 边分别在
边分别在![]() 轴、
轴、![]() 轴的正半轴上,
轴的正半轴上, ![]() 点与坐标原点重合,将矩形折叠,使
点与坐标原点重合,将矩形折叠,使![]() 点落在线段
点落在线段![]() 上,设此点为
上,设此点为![]() .
.
(1)若折痕的斜率为-1,求折痕所在的直线的方程;
(2)若折痕所在直线的斜率为![]() ,(
,( ![]() 为常数),试用
为常数),试用![]() 表示点
表示点![]() 的坐标,并求折痕所在的直线的方程;
的坐标,并求折痕所在的直线的方程;
(3)当![]() 时,求折痕长的最大值.
时,求折痕长的最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某学校高三年级共800名男生中随机抽取50名测量身高,测量发现被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160);第二组[160,165)、…、第八组[190,195],下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
(1)估计这所学校高三年级全体男生身高180cm以上(含180cm)的人数;
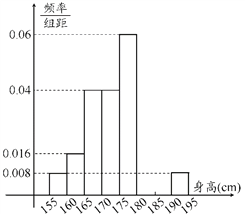
(2)求第六组、第七组的频率并补充完整频率分布直方图(如需增加刻度请在纵轴上标记出数据,并用直尺作图);
(3)由直方图估计男生身高的中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,经过点
中,经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 有两个不同的交点
有两个不同的交点![]() 和
和![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)设椭圆与![]() 轴正半轴、
轴正半轴、![]() 轴正半轴的交点分别为
轴正半轴的交点分别为![]() ,是否存在常数
,是否存在常数![]() ,使得向量
,使得向量![]() 与
与![]() 共线?如果存在,求
共线?如果存在,求![]() 值;如果不存在,请说明理由.
值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,直线
,直线![]() 交此抛物线于不同的两个点
交此抛物线于不同的两个点![]() 、
、![]() .
.
(![]() )当直线
)当直线![]() 过点
过点![]() 时,证明
时,证明![]() ,
,![]() 为定值.
为定值.
(![]() )当
)当![]() 时,直线
时,直线![]() 是否过定点?若过定点,求出定点坐标;反之,请说明理由.
是否过定点?若过定点,求出定点坐标;反之,请说明理由.
(![]() )记
)记![]() ,如果直线
,如果直线![]() 过点
过点![]() ,设线段
,设线段![]() 的中点为
的中点为![]() ,线段
,线段![]() 的中点为
的中点为![]() .问是否存在一条直线和一个定点,使得点
.问是否存在一条直线和一个定点,使得点![]() 到它们的距离相等?若存在,求出这条直线和这个定点;若不存在,请说明理由.
到它们的距离相等?若存在,求出这条直线和这个定点;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与
与![]() 轴负半轴相交于点
轴负半轴相交于点![]() ,与
,与![]() 轴正半轴相交于点
轴正半轴相交于点![]() .
.
(1)若过点 的直线
的直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若在以![]() 为圆心半径为
为圆心半径为![]() 的圆上存在点
的圆上存在点![]() ,使得
,使得![]() (
(![]() 为坐标原点),求
为坐标原点),求![]() 的取值范围;
的取值范围;
(3)设![]() 是圆
是圆![]() 上的两个动点,点
上的两个动点,点![]() 关于原点的对称点为
关于原点的对称点为![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,如果直线
,如果直线![]() 与
与![]() 轴分别交于
轴分别交于![]() 和
和![]() ,问
,问![]() 是否为定值?若是求出该定值;若不是,请说明理由.
是否为定值?若是求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图,梯形![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,
,![]() ,
,![]() ,将
,将![]() 沿对角线
沿对角线![]() 折起.设折起后点
折起.设折起后点![]() 的位置为
的位置为![]() ,并且平面
,并且平面![]()
![]() 平面
平面![]() .给出下面四个命题:
.给出下面四个命题:
①![]() ;②三棱锥
;②三棱锥![]() 的体积为
的体积为![]() ;③
;③![]()
![]() 平面
平面![]() ;
;
④平面![]() 平面
平面![]() .其中正确命题的序号是( )
.其中正确命题的序号是( )


A. ①② B. ③④ C. ①③ D. ②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com