
| A. | ($\frac{1}{7}$,$\frac{1}{5}$]∪(5,7] | B. | ($\frac{1}{5}$,$\frac{1}{3}$]∪(5,7] | C. | ($\frac{1}{5}$,$\frac{1}{3}$]∪(3,5] | D. | ($\frac{1}{7}$,$\frac{1}{5}$]∪(3,5] |
分析 本题通过典型的作图画出loga|x|以及f(x)的图象,从图象交点上交点的不同,来判断函数零点个数,从而确定底数a的大小范围.
解答 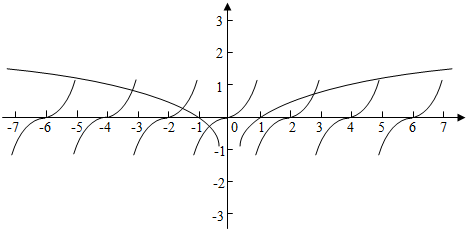 解:首先将函数g(x)=f(x)-loga|x|恰有6个零点,这个问题转化成f(x)=loga|x|的交点来解决.
解:首先将函数g(x)=f(x)-loga|x|恰有6个零点,这个问题转化成f(x)=loga|x|的交点来解决.
数形结合:如图,f(x+2)=f(x),知道周期为2,当-1<x≤1时,f(x)=x3图象可以画出来,同理左右平移各2个单位,得到在(-7,7)上面的图象,
以下分两种情况:
(1)当a>1时,loga|x|如图所示,左侧有4个交点,右侧2个,
此时应满足loga5≤1<loga7,即loga5≤logaa<loga7,所以5≤a<7.
(2)当0<a<1时,loga|x|与f(x)交点,左侧有2个交点,右侧4个,
此时应满足loga5>-1,loga7≤-1,即loga5<-logaa≤loga7,所以5<a-1≤7.故$\frac{1}{7}$≤a<$\frac{1}{5}$综上所述,a的取值范围是:5≤a<7或$\frac{1}{7}$≤a<$\frac{1}{5}$,
故选:A.
点评 本题考查函数零点应用转化为两个函数交点来判断,又综合了奇函数对称性对数运算等知识,属于较难的一类题,端点也要认真考虑,极容易漏掉端点.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
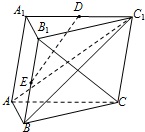 如图,在三棱柱ABC-A1B1C1中,D,E分别为A1C1,BB1的中点,B1C⊥AB,侧面BCC1B1为菱形.求证:
如图,在三棱柱ABC-A1B1C1中,D,E分别为A1C1,BB1的中点,B1C⊥AB,侧面BCC1B1为菱形.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$ | B. | $-\frac{2}{5}$ | C. | $±\frac{2}{5}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{9}-\frac{y^2}{27}=1$ | B. | $\frac{y^2}{9}-\frac{x^2}{27}=1$ | C. | $\frac{y^2}{27}-\frac{x^2}{9}=1$ | D. | $\frac{x^2}{27}-\frac{y^2}{9}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
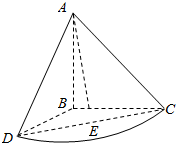 等腰直角三角形ABC中,AB=BC=2,将斜边AC绕直角边AB旋转90°后得到旋转体A-BCD,如图所示,求:
等腰直角三角形ABC中,AB=BC=2,将斜边AC绕直角边AB旋转90°后得到旋转体A-BCD,如图所示,求:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com