练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．读程序

    对甲乙两程序和输出结果判断正确的是（　　）
    A．程序不同，结果不同B．程序相同，结果不同
    C．程序不同，结果相同D．程序相同，结果相同

    分析 程序甲是WHILE WEND语句，只要变量i≤100成立，求和运算就要执行下去，直到i＞100时终止运算并输出求出的和S；而程序乙是DO LOOP UNTIL语句，只要变量i≥1成立，求和运算就要执行下去，直到i＜1时终止运算并输出求出的和S，由此可得两程序结构不同，但输出的S相同，可得本题答案．

    解答 解：程序甲是计数变量i从1开始逐步递增直到i=100时终止，
    变量S从1开始，这个程序计算的是：1×4×7×…×100；
    程序乙计数变量i从100开始逐步递减到i=2时终止，
    变量S从100开始，这个程序计算的是100×97×94×…×1．
    但这两个程序是不同的．两种程序的输出结果相同．
    故选：C．

    点评 本题给出两个伪代码语段，要我们比较它们的异同，着重考查了循环结构的理解和伪代码程序的逻辑处理等知识，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

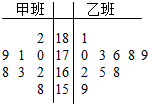    17．随机抽取某中学甲乙两班各10名同学，测量他们的身高（单位：cm），获得身高数据的茎叶图如图示，根据茎叶图解答下列问题；
    （1）计算甲班与乙班的身高数据的中位数．
    （2）判断哪个班的平均身高较高．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．数列{an}，an≥0，a1=0，an+12+an+1-1=an2，n∈N*．
    （1）求证：an＜1；
    （2）求证：数列{an}递增；
    （3）求证：$\frac{1}{1+{a}_{1}}$+$\frac{1}{（1+{a}_{1}）（1+{a}_{2}）}$+…+$\frac{1}{（1+{a}_{1}）（1+{a}_{2}）…（1+{a}_{n}）}$＜3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

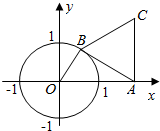    15．如图的平面直角坐标系中，O为坐标原点，点B在单位圆上，A（2，0），∠AOB=θ，△ABC为等边三角形．
    （1）若直线OB的斜率为$\frac{2}{3}$，求$\frac{si{n}^{2}θ-sin2θ}{co{s}^{2}θ+cos2θ}$的值；
    （2）若θ∈（0，π），求四边形OACB面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．教育储蓄是一种零存整取定期储蓄存款，它享受整存整取利率，利息免税，教育储蓄的对象为在校小学四年级（含四年级）以上的学生．假设零存整取3年期教育储蓄的月利率为千分之两点一．
    （1）欲在3年后一次支取本息合计2万元，每月大约存入多少元？
    （2）零存整取3年期教育储蓄每月至多存入多少元，3年后本息合计约为5万元（精确到1元）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．直线ax+4y-a=0与直线6x+8y+5=0平行，则这两直线间的距离为1.1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．不等式$\frac{3{x}^{2}+2x+2}{{x}^{2}+x+1}≥m$对任意实数x都成立，则实数m的取值范围是m≤2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．如果指数函数y=ax（a＞0且a≠1）在x∈[0，1]上的最大值与最小值的和为$\frac{5}{2}$，则实数a=$\frac{3}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．在△ABC中，AB=2，AC=3，BC边上的中线AD=2，则△ABC的面积为$\frac{3\sqrt{15}}{4}$．

    查看答案和解析>>

    同步练习册答案