练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】若定义在上的偶函数满足，且在区间上是减函数，，现有下列结论，其中正确的是：（ ）

    ①的图象关于直线对称；②的图象关于点对称；③在区间上是减函数；④在区间内有8个零点.

    A.①③B.②④C.①③④D.②③④

    【答案】C

    【解析】

    根据题意可得，再由函数为偶函数可得，从而可判断①；无法推出，可判断②；利用周期为2可判断③；利用对称性可判断④.

    由，得，

    结合为偶函数，得，

    则曲线关于直线对称，则①正确；

    无法推出，则②不一定正确；

    由曲线可得曲线，

    即得曲线，恰好是在一个周期内的图象；

    再根据是以2为周期的函数，得到曲线，

    因为在在上是减函数，在上是减函数，则③正确；

    因为在上是减函数，，，

    所以在上有唯一的一个零点，

    根据对称性，在区间内有8个零点.

    故选：C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知四棱锥的底面ABCD是边长为3的正方形，平面ABCD，，E为PD中点，过EB作平面分别与线段PA、PC交于点M，N，且，则________；四边形EMBN的面积为________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线 ，其焦点到准线的距离为2，直线与抛物线交于，两点，过，分别作抛物线的切线，，与交于点.

    （Ⅰ）求的值；

    （Ⅱ）若，求面积的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在正三棱柱中，，，点，满足，.

    （1）证明：面；

    （2）求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在中，内角A，B，C的对边分别为a，b，c，且.

    （1）若，，请判断的形状；

    （2）若，求面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱中，平面为等边三角形，为的中点，为上的点，且．

    （1）求证：平面平面；

    （2）求直线与平面所成角的正切值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出下列结论：

    ①下面程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图，若输入的，分别为8，12，则输出的；

    ②若用样本数据0，－1，2，3来估计总体的标准差，则总体的标准差估计值为；

    ③命题：“若，则”的否命题是“若，则”；

    ④已知正数，满足，则的最大值是；

    ⑤已知函数满足，，且当时，.则在区间为增函数.

    其中结论正确的序号是______.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

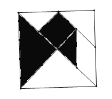
    【题目】七巧板是中国古代劳动人民的发明，其历史至少可以追溯到公元前一世纪，后清陆以湉《冷庐杂识》卷一中写道“近又有七巧图，其式五，其数七，其变化之式多至千余”在18世纪，七巧板流传到了国外，被誉为“东方魔板”，至今英国剑桥大学的图书馆里还珍藏着一部《七巧新谱》．完整图案为一正方形(如图)：五块等腰直角三角形、一块正方形和一块平行四边形，如果在此正方形中随机取一点，那么此点取自阴影部分的概率是（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一个盒中有形状、大小、质地完全相同的5张扑克牌，其中3张红桃，1张黑桃，1张梅花．现从盒中一次性随机抽出2张扑克牌，则这2张扑克牌花色不同的概率为

    A. B. C. D.

    查看答案和解析>>

    同步练习册答案