
(Ⅰ)求动点Q的轨迹方程;
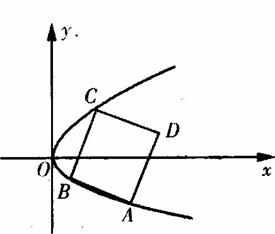
(Ⅱ)若正方形ABCD的三个顶点A、B、C在点Q的轨迹上,求正方形ABCD面积的最小值.
解:(1)设Q(x,y),因为![]() ,所以N(0,
,所以N(0,![]() ),
),
又M(-3m,0),所以![]() =(3m,
=(3m,![]() ),
),![]() =(x,
=(x,![]() ),
),
由已知![]() =0,则3mx
=0,则3mx![]() y2=0,y2=4mx.
y2=0,y2=4mx.
即Q点轨迹方程为y2=4mx.
(Ⅱ)如图,不妨设正方形在抛物线上的三个顶点中A、B在x轴的下方(包括x轴),记A、B、C的坐标分别为(x1,y1),(x2,x2),(x3,y3),其中y3>0≥y2>y1并设直线AB的斜率为k(k<0)
则有 ①
①

又因为A、B、C在抛物线y2=4mx上,故有x1=![]() ,x2=
,x2=![]() ,x3=
,x3=![]() 代入①式得
代入①式得
y1=![]() y2,y3=-4mk-y2 ②
y2,y3=-4mk-y2 ②
∵|AB|=|BC|即![]()
∴![]() (y2-y1)=
(y2-y1)=![]() (y3-y2)
(y3-y2)
∴(y2-y1)=-k(y3-y2)将②代入可得:y2![]() +y2=-k(-4mk-2y2)
+y2=-k(-4mk-2y2)
即-4mk2-=-2(-k+1)y2,得y2=
正方形的边长为|AB|![]() =(y3-y2)=
=(y3-y2)=![]() (-4mk-2y2)
(-4mk-2y2)
=![]() (-4mk
(-4mk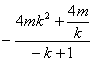 )=4m
)=4m![]() [-k-
[-k-![]() ]=4m
]=4m![]()
易知![]() 所以4m
所以4m![]()
所以正方形ABCD面积的最小值为32m2


科目:高中数学 来源:天利38套《2008全国各省市高考模拟试题汇编 精华大字版》、数学理 题型:044
如图,已知M(-3m,0)(m>0),N、P两点分别在y轴和x轴上运动,并且满足![]() ·
·![]() =0,
=0,![]() =
=![]()
![]() .
.

(Ⅰ)求动点Q的轨迹方程;
(Ⅱ)若正方形ABCD的三个顶点A、B、C在点Q的轨迹上,求正方形ABCD面积的最小值.
查看答案和解析>>
科目:高中数学 来源:天利38套《2008全国各省市高考模拟试题汇编 精华大字版》、数学文 精华大字版 题型:044
如图,已知M(-3m,0)(m>0),N、P两点分别在y轴和x轴上运动,并且满足![]()

(Ⅰ)求动点Q的轨迹方程;
(Ⅱ)若正方体ABCD的三个顶点A、B、C在点Q的轨迹上,求正方形ABCD面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
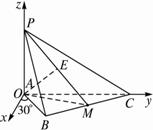
(1)画出这个空间直角坐标系,并指出![]() 与Ox的轴的正方向的夹角;
与Ox的轴的正方向的夹角;
(2)求证:![]() ⊥
⊥![]() ;
;
(3)若M为BC的中点,n=![]() m,求直线AM与平面PBC所成角的大小.
m,求直线AM与平面PBC所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
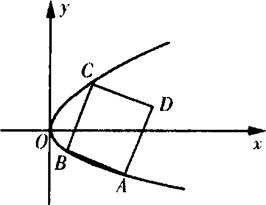
(Ⅰ)求动点Q的轨迹方程;
(Ⅱ)若正方体ABCD的三个顶点A、B、C在点Q的轨迹上,求正方形ABCD面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com