
【题目】已知直线l的参数方程为 ![]() (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为2ρ2﹣ρ2cos2θ=12.若曲线C的左焦点F在直线l上,且直线l与曲线C交于A,B两点.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为2ρ2﹣ρ2cos2θ=12.若曲线C的左焦点F在直线l上,且直线l与曲线C交于A,B两点.
(1)求m的值并写出曲线C的直角坐标方程;
(2)求 ![]() 的值.
的值.
【答案】
(1)解:直线l的参数方程为 ![]() (t为参数),消去参数t可得普通方程:x﹣y=m.
(t为参数),消去参数t可得普通方程:x﹣y=m.
曲线C的极坐标方程为2ρ2﹣ρ2cos2θ=12.可得曲线C的直角坐标方程:2(x2+y2)﹣(x2﹣y2)=12,
∴曲线C的标准方程为 ![]() ,则其左焦点为
,则其左焦点为 ![]() ,
,
故 ![]() ,曲线C的方程
,曲线C的方程 ![]()
(2)解:直线l的参数方程为 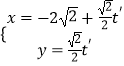 ,与曲线C的方程
,与曲线C的方程 ![]() 联立,
联立,
得t'2﹣2t'﹣2=0,则|FA||FB|=|t'1t'2|=2,
![]() ,
,
故 ![]()
【解析】(1)直线l的参数方程为 ![]() (t为参数),消去参数t可得普通方程.曲线C的极坐标方程为2ρ2﹣ρ2cos2θ=12.利用互化公式可得曲线C的直角坐标方程,可得其左焦点,即可得出m.(2)直线l的参数方程为
(t为参数),消去参数t可得普通方程.曲线C的极坐标方程为2ρ2﹣ρ2cos2θ=12.利用互化公式可得曲线C的直角坐标方程,可得其左焦点,即可得出m.(2)直线l的参数方程为 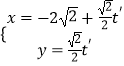 ,与曲线C的方程
,与曲线C的方程 ![]() 联立,利用根与系数的关系、弦长公式即可得出.
联立,利用根与系数的关系、弦长公式即可得出.


科目:高中数学 来源: 题型:
【题目】某乐队参加一户外音乐节,准备从3首原创新曲和5首经典歌曲中随机选择4首进行演唱.
(1)求该乐队至少演唱1首原创新曲的概率;
(2)假定演唱一首原创新曲观众与乐队的互动指数为a(a为常数),演唱一首经典歌曲观众与乐队的互动指数为2a,求观众与乐队的互动指数之和X的概率分布及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校的平面示意图为如下图五边形区域ABCDE,其中三角形区域ABE为生活区,四边形区域BCDE为教学区,AB,BC,CD,DE,EA,BE为学校的主要道路(不考虑宽度). ![]() ,
, ![]() .
. 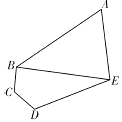
(1)求道路BE的长度;
(2)求生活区△ABE面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,点A、B是函数f(x)图象上不同两点,则∠AOB(O为坐标原点)的取值范围是( )
,点A、B是函数f(x)图象上不同两点,则∠AOB(O为坐标原点)的取值范围是( )
A.(0, ![]() )
)
B.(0, ![]() ]
]
C.(0, ![]() )
)
D.(0, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为![]() 的正方体
的正方体![]() 中,点
中,点![]() 是棱
是棱![]() 的中点,点
的中点,点![]() 在棱
在棱![]() 上,且满足
上,且满足![]() .
.

(1)求证:![]() ;
;
(2)在棱![]() 上确定一点
上确定一点![]() ,使
,使![]() 、
、![]() 、
、![]() 、
、![]() 四点共面,并求此时
四点共面,并求此时![]() 的长;
的长;
(3)求平面![]() 与平面
与平面![]() 所成二面角的余弦值.
所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 对任意n∈N+ , Sn=(﹣1)nan+ ![]() +n﹣3且(t﹣an+1)(t﹣an)<0恒成立,则实数t的取值范围是 .
+n﹣3且(t﹣an+1)(t﹣an)<0恒成立,则实数t的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某社区居民有无收看“奥运会开幕式”,某记者分别从某社区60~70岁,40~50岁,20~30岁的三个年龄段中的160人,240人,x人中,采用分层抽样的方法共抽查了30人进行调查,若在60~70岁这个年龄段中抽查了8人,那么x为( ) .
A. 90 B. 120 C. 180 D. 200
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com