
()(本小题满分13分)
设椭圆![]() 过点
过点![]() ,且着焦点为
,且着焦点为![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)当过点![]() 的动直线
的动直线![]() 与椭圆
与椭圆![]() 相交与两不同点
相交与两不同点![]() 时,在线段
时,在线段![]() 上取点
上取点![]() ,满足
,满足![]() ,证明:点
,证明:点![]() 总在某定直线上
总在某定直线上
科目:高中数学 来源:2012-2013学年广东省惠州市高一上学期期中考试数学试卷(解析版) 题型:解答题
(本小题满分13分)已知函数 经过点
经过点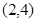 .
.
(1)求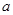 的值;(2)求
的值;(2)求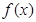 在[0,1]上的最大值与最小值.
在[0,1]上的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年重庆市高三11月月考文科数学 题型:解答题
(本小题满分13分,(Ⅰ)小问6分,(Ⅱ)小问7分. )
已知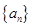 是首项为19,公差为-2的等差数列,
是首项为19,公差为-2的等差数列,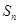 为
为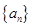 的前
的前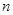 项和.
项和.
(Ⅰ)求通项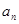 及
及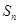 ;
;
(Ⅱ)设 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列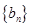 的通项公式及其前
的通项公式及其前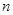 项和
项和 .
.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年重庆市高三11月月考文科数学 题型:解答题
(本小题满分13分,(Ⅰ)小问7分,(Ⅱ)小问6分.)
设函数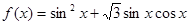

(1)求 的最小正周期和值域;
的最小正周期和值域;
(2)将函数 的图象按向量
的图象按向量 平移后得到函数
平移后得到函数 的图
象,求函数
的图
象,求函数 的单调区间。
的单调区间。
查看答案和解析>>
科目:高中数学 来源:湖南省长沙市2010-2011学年高三年级月考(一)数学试题(理科) 题型:解答题
(本小题满分13分)
已知 是二次函数,不等式
是二次函数,不等式 的解集是(0,5),且
的解集是(0,5),且 在区间[-1,4]上的最大值是12。
在区间[-1,4]上的最大值是12。
(1)求 的解析式;
的解析式;
(2)是否存在自然数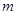 ,使得方程
,使得方程 在区间
在区间 内有且只有两个不等的实数根?若存在,求出
内有且只有两个不等的实数根?若存在,求出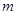 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省莆田市高三毕业班适应性练习理科数学 题型:解答题
(本小题满分13分)
随机变量X的分布列如下表如示,若数列 是以
是以 为首项,以
为首项,以 为公比的等比数列,则称随机变量X服从等比分布,记为Q(
为公比的等比数列,则称随机变量X服从等比分布,记为Q( ,
, ).现随机变量X∽Q(
).现随机变量X∽Q( ,2).
,2).
|
X |
1 |
2 |
… |
n |
|
|
|
|
… |
|
(Ⅰ)求n 的值并求随机变量X的数学期望EX;
(Ⅱ)一个盒子里装有标号为1,2,…,n且质地相同的标签若干张,从中任取1张标签所得的标号为随机变量X.现有放回的从中每次抽取一张,共抽取三次,求恰好2次取得标签的标号不大于3的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com