
| A. | (-∞,3-2ln2] | B. | [3-2ln2,+∞) | C. | [$\sqrt{e}$,+∞) | D. | (-∞,$-\sqrt{e}$] |
分析 画出函数f(x)的图象,求出函数g(x)=$\frac{1}{2}$(|x+a|+1)的最小值,利用已知条件转化列出不等式求解即可.
解答 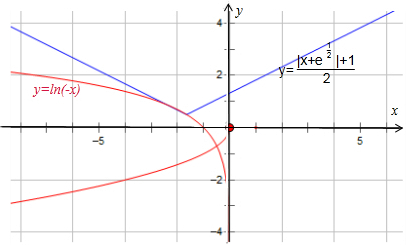 解:函数f(x)=$\left\{\begin{array}{l}{lnx(x>0)}\\{-\sqrt{-x}(x≤0)}\end{array}\right.$的图象如图:
解:函数f(x)=$\left\{\begin{array}{l}{lnx(x>0)}\\{-\sqrt{-x}(x≤0)}\end{array}\right.$的图象如图:
g(x)=$\frac{1}{2}$(|x+a|+1)$≥\frac{1}{2}$,当且仅当x=-a时取等号,
函数y=ln(-x)与y=$\frac{1}{2}$(|x+$\sqrt{e}$|+1)在x<0有解,而且g(x)=$\frac{1}{2}$(|x+a|+1)看作g(x)=$\frac{1}{2}$(|x|+1)向左平移而得,y′=[ln(-x)]′=$\frac{1}{x}$,可得切点横坐标为:$\frac{1}{x}=-\frac{1}{2}$,即x=-2,
此时a取得最小值:ln2=$\frac{1}{2}$(|-2+a|+1),解得a=3-2ln2.
函数f(x)=$\left\{\begin{array}{l}{lnx(x>0)}\\{-\sqrt{-x}(x≤0)}\end{array}\right.$与g(x)=$\frac{1}{2}$(|x+a|+1)的图象上存在关于y轴对称的点,
所以实数a的取值范围是:[3-2ln2,+∞).
故选:B.
点评 本题考查函数的零点,函数的图象的画法,考查数形结合以及转化思想的应用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 不存在x0∈R+,使log2x0>0 | B. | 对任意的x∈R+,有log2x>0 | ||
| C. | 对任意的x∈R+,有log2x≤0 | D. | 存在x0∈R+,使log2x0>0 |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省南昌市高一下学期期末考试数学试卷(解析版) 题型:选择题
下列四个命题:
①样本方差反映的是所有样本数据与样本平均值的偏离程度;
②某校高三一级部和二级部的人数分别是m、n,本次期末考试两级部数学平均分分别是a、b,则这两个级部的数学平均分为
③某中学采用系统抽样方法,从该校高一年级全体800名学生中抽50名学生做牙齿健康检查,现将800名学生从001到800进行编号,已知从497--512这16个数中取得的学生编号是503,则初始在第1小组00l~016中随机抽到的学生编号是007.
其中命题正确的个数是( )
A.0个 B.1个 C.2个 D.3个
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省南昌市高一下学期期末考试数学试卷(解析版) 题型:选择题
在△ABC中,已知a=8,B=60°,C=75°,则b等于( )
A.4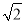 B.4
B.4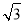 C.4
C.4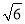 D.
D.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省南昌市高二理下学期期末考试数学试卷(解析版) 题型:选择题
若函数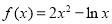 在其定义域的一个子区间
在其定义域的一个子区间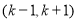 内不是单调函数,则实数
内不是单调函数,则实数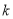 的取值范围是( )
的取值范围是( )
A.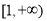 B.
B.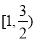 C.
C. D.
D.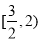
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com