考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)连结BD,得EF∥BD,又BD∥B1D1,所以EF∥B1D1,由此能证明直线EF∥平面CB1D1.
(2)由已知得A1C1⊥B1D1,CC1⊥平面A1B1C1D1,从而CC1⊥B1D1,由此能证明B1D1⊥平面CAA1C1,从而能证明平面CAA1C1⊥平面CB1D1.
解答:
(1)证明:连结BD,在△ABD中,
E、F分别为棱AD、AB的中点,故EF∥BD,
又BD∥B1D1,所以EF∥B1D1,…(2分)
又B1D1?平面CB1D1,EF不包含于平面CB1D1,
所以直线EF∥平面CB1D1.…(6分)
(2)证明:在正方体ABCD-A1B1C1D1中,底面A1B1C1D1是正方形,
则A1C1⊥B1D1…(8分)
又CC1⊥平面A1B1C1D1,B1D1?平面A1B1C1D1,
则CC1⊥B1D1,…(10分)
又A1C1∩CC1=C1,A1C1?平面CAA1C1,CC1?平面CAA1C1,
所以B1D1⊥平面CAA1C1,又B1D1?平面CB1D1,
所以平面CAA1C1⊥平面CB1D1.…(12分)
点评:本题考查直线与平面平行的证明,考查平面与平面垂直的证明,解题时要认真审题,注意空间思维能力的培养.

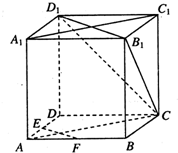 如图,在正方体ABCD-A1B1C1D1中,E、F分别为AD,AB的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别为AD,AB的中点.

 出彩同步大试卷系列答案
出彩同步大试卷系列答案 如图,正方形ABCD中,E,F分别是AB,BC的中点,O是EF的中点,现在沿DE,DF及EF把这个正方形折成一个四面体,使A,B,C三点重合,重合后的点记为G,则在四面体D-EFG中必有( )
如图,正方形ABCD中,E,F分别是AB,BC的中点,O是EF的中点,现在沿DE,DF及EF把这个正方形折成一个四面体,使A,B,C三点重合,重合后的点记为G,则在四面体D-EFG中必有( )