
(12分)如下图是一个方格迷宫,甲、乙两人分别位于迷宫的A、B两处,两人同时以每分钟一格的速度向东、西、南、北四个方向行走,已知甲向东、西行走的概率都为![]() ,向南、北行走的概率为
,向南、北行走的概率为![]() 和p,乙向东、西、南、北四个方向行走的概率均为q.
和p,乙向东、西、南、北四个方向行走的概率均为q.
(1)求p和q的值;
(2)问最少几分钟,甲乙二人相遇?并求出最短时间内可以相遇的概率.

科目:高中数学 来源: 题型:
(本小题满分12分)
有一幅椭圆型彗星轨道图,长4cm,高![]() ,如下图,
,如下图,
已知O为椭圆中心,A1,A2是长轴两端点,
|
(Ⅰ)建立适当的坐标系,写出椭圆方程,
并求出当彗星运行到太阳正上方时二者在图上的距离;
(Ⅱ)直线l垂直于A1A2的延长线于D点,|OD|=4,
设P是l上异于D点的任意一点,直线A1P,A2P分别
交椭圆于M、N(不同于A1,A2)两点,问点A2能否
在以MN为直径的圆上?试说明理由.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省信阳市毕业班第一次调研考试文科数学试卷 题型:解答题
(本小题满分12分)请你设计一个包装盒,如下图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A、B、C、D四个点重合于图中的点P,正好形成一个正四棱挪状的包装盒E、F在AB上,是被切去的一等腰直角三角形斜边的两个端点.设AE= FB=x(cm).

(I)某广告商要求包装盒的侧面积S(cm2)最大,试问x应取何值?
(II)某厂商要求包装盒的容积V(cm3)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值.[
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成
 六段,
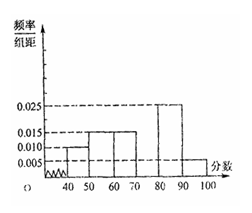
六段,![]() 后画出如下图的频率分布直方图,观察图形,回答下列问题:
后画出如下图的频率分布直方图,观察图形,回答下列问题:
(Ⅰ)求第四小组的频率,并补全这个频率
分布直方图;
(Ⅱ)估计这次考试的合格率(60分及60分以上为合格);
(Ⅲ)把90分以上(包括90分)视为成绩
优秀,那么从成绩是60分以上(包括60分)
的学生中选一人,求此人成绩优秀的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
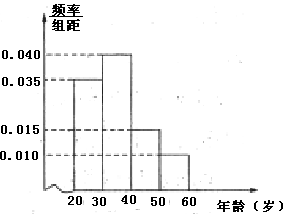
(本小题满分12分)某工厂有120名工人,其年龄都在20~60岁之间,各年龄段人数按[20,30),[30,40),[40,50),[50,60]分组,其频率分布直方图如下图所示.工厂为了开发新产品,引进了新的生产设备,要求每个工人都要参加A、B两项培训,培训结束后进行结业考试,已知各年龄段两项培训结业考试成绩优秀的人数如下表所示.假设两项培训是相互独立的,结业考试也互不影响。
| 年龄分组 | A项培训成绩优秀人数 | B项培训成绩优秀人数 |
| [20,30) | 30 | 18 |
| [30,40) | 36 | 24 |
| [40,50) | 12 | 9 |
| [50,60] | 4 | 3 |
(1)若用分层抽样法从全厂工人中抽取一个容量为40的样本,求各年龄段应分别抽取的人数,并估计全厂工人的平均年龄;
(2)随机从年龄段[20,30)和[30,40)中各抽取1人,求这两人中至少有一人在A、B两项培训结业考试成绩为优秀的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com