
【题目】已知数列{an}满足a1=1,且an+1﹣an=2n , n∈N* , 若 ![]() +19≤3n对任意n∈N*都成立,则实数λ的取值范围为 .
+19≤3n对任意n∈N*都成立,则实数λ的取值范围为 .
【答案】(﹣∞,﹣8]
【解析】解:∵a1=1,且an+1﹣an=2n , n∈N* , 即n≥2时,an﹣an﹣1=2n﹣1 . ∴an=(an﹣an﹣1)+(an﹣1﹣an﹣2)+…+(a2﹣a1)+a1=2n﹣1+2n﹣2+…+2+1= ![]() =2n﹣1.
=2n﹣1.
∵ ![]() +19≤3n,化为:λ≤
+19≤3n,化为:λ≤ ![]() =f(n).
=f(n).![]() +19≤3n对任意n∈N*都成立,λ≤f(n)min .
+19≤3n对任意n∈N*都成立,λ≤f(n)min .
由f(n)≤0,可得n≤ ![]() ,因此n≤6时,f(n)<0;n≥7时,f(n)>0.
,因此n≤6时,f(n)<0;n≥7时,f(n)>0.
f(n+1)﹣f(n)= ![]() ﹣
﹣ ![]() =
= ![]() ≤0,
≤0,
解得n≤ ![]() .
.
∴f(1)>f(2)>f(3)>f(4)>f(5)<f(6),
可得f(n)min=f(5)=﹣8.
则实数λ的取值范围为(﹣∞,﹣8].
故答案为:(﹣∞,﹣8].
a1=1,且an+1﹣an=2n , n∈N* , 即n≥2时,an﹣an﹣1=2n﹣1 . 利用an=(an﹣an﹣1)+(an﹣1﹣an﹣2)+…+(a2﹣a1)+a1可得an. ![]() +19≤3n,化为:λ≤
+19≤3n,化为:λ≤ ![]() =f(n).
=f(n). ![]() +19≤3n对任意n∈N*都成立,λ≤f(n)min . 通过作差即可得出最小值.
+19≤3n对任意n∈N*都成立,λ≤f(n)min . 通过作差即可得出最小值.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
【题目】为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表和频率分布直方图:
月工资 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
男员工数 | 1 | 8 | 10 | 6 | 4 | 4 |
女员工数 | 4 | 2 | 5 | 4 | 1 | 1 |

(1)试由图估计该单位员工月平均工资;
(2)现用分层抽样的方法从月工资在[45,55)和[55,65)的两组所调查的男员工中随机选取5人,问各应抽取多少人?
(3)若从月工资在[25,35)和[45,55)两组所调查的女员工中随机选取2人,试求这2人月工资差不超过1000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的方程为(2﹣m)x+(2m+1)y+3m+4=0,其中m∈R.
(1)求证:直线l恒过定点;
(2)当m变化时,求点P(3,1)到直线l的距离的最大值;
(3)若直线l分别与x轴、y轴的负半轴交于A,B两点,求△AOB面积的最小值及此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的各项均为正数,记数列{an}的前n项和为Sn,数列{an2}的前n项和为Tn,且3Tn=Sn2+2Sn,n∈N*.
(Ⅰ)求a1的值;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)若k,t∈N*,且S1,Sk-S1,St-Sk成等比数列,求k和t的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点. 
(1)证明:BE⊥DC;
(2)求直线BE与平面PBD所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在圆内接△ABC,A,B,C所对的边分别为a,b,c,满足acosC+ccosA=2bcosB. 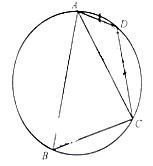
(1)求B的大小;
(2)若点D是劣弧 ![]() 上一点,AB=3,BC=2,AD=1,求四边形ABCD的面积.
上一点,AB=3,BC=2,AD=1,求四边形ABCD的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
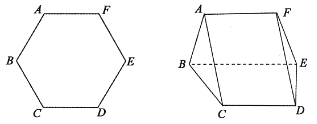
【题目】如图,将边长为2的正六边形ABCDEF沿对角线BE翻折,连接AC、FD,形成如图所示的多面体,且![]() ,(1)证明:平面ABEF
,(1)证明:平面ABEF![]() 平面BCDE; (2)求DE与平面ABC所成角的正弦值。
平面BCDE; (2)求DE与平面ABC所成角的正弦值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com