
【题目】设实数x,y满足不等式组  ,(2,1)是目标函数z=﹣ax+y取最大值的唯一最优解,则实数a的取值范围是( )
,(2,1)是目标函数z=﹣ax+y取最大值的唯一最优解,则实数a的取值范围是( )
A.(0,1)
B.(0,1]
C.(﹣∞,﹣2)
D.(﹣∞,﹣2]
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】抛物线![]() (
(![]() )的焦点为
)的焦点为![]() ,已知点
,已知点![]() ,
, ![]() 为抛物线上的两个动点,且满足
为抛物线上的两个动点,且满足![]() .过弦
.过弦![]() 的中点
的中点![]() 作抛物线准线的垂线
作抛物线准线的垂线![]() ,垂足为
,垂足为![]() ,则
,则![]() 的最大值为__________.
的最大值为__________.
【答案】1
【解析】设![]() ,在三角形ABF中,用余弦定理得到
,在三角形ABF中,用余弦定理得到![]()
![]() ,
, 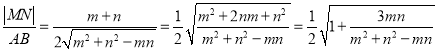
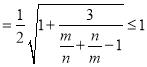 故最大值为1.
故最大值为1.
故答案为:1.
点睛:本题主要考查了抛物线的简单性质.解题的关键是利用了抛物线的定义。一般和抛物线有关的小题,很多时可以应用结论来处理的;平时练习时应多注意抛物线的结论的总结和应用。尤其和焦半径联系的题目,一般都和定义有关,实现点点距和点线距的转化。
【题型】填空题
【结束】
17
【题目】设![]() 的内角
的内角![]() ,
, ![]() ,
, ![]() 所对的边分别为
所对的边分别为![]() ,
, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() .
.
(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)当![]() 的面积为
的面积为![]() 时,求
时,求![]() 的周长.
的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为奇函数,
为奇函数,![]() 为偶函数,且
为偶函数,且![]() .
.
(Ⅰ)求函数![]() 及
及![]() 的解析式;
的解析式;
(Ⅱ)用函数单调性的定义证明:函数![]() 在
在![]() 上是减函数;
上是减函数;
(Ⅲ)若关于![]() 的方程
的方程![]() 有解,求实数
有解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
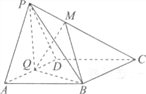
(Ⅰ)若PA=PD,求证:平面PQB⊥平面PAD;
(Ⅱ)点M在线段PC上,PM=tPC,试确定实数t的值,使PA∥平面MQB;
(Ⅲ)在(Ⅱ)的条件下,若平面PAD⊥平面ABCD,且PA=PD=AD=2,求二面角M-BQ-C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (a>b>0)的焦点在圆x2+y2=3上,且离心率为
(a>b>0)的焦点在圆x2+y2=3上,且离心率为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过原点O的直线l与椭圆C交于A,B两点,F为右焦点,若△FAB为直角三角形,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运输公司有7辆可载![]() 的
的![]() 型卡车与4辆可载
型卡车与4辆可载![]() 的
的![]() 型卡车,有9名驾驶员,建筑某段高速公路中,此公司承包了每天至少搬运
型卡车,有9名驾驶员,建筑某段高速公路中,此公司承包了每天至少搬运![]() 沥青的任务,已知每辆卡车每天往返的次数为
沥青的任务,已知每辆卡车每天往返的次数为![]() 型车8次,
型车8次, ![]() 型车6次,每辆卡车每天往返的成本费为
型车6次,每辆卡车每天往返的成本费为![]() 型车160元,
型车160元, ![]() 型车252元,每天派出
型车252元,每天派出![]() 型车和
型车和![]() 型车各多少辆,公司所花的成本费最低?
型车各多少辆,公司所花的成本费最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AC⊥AB,AD⊥DC,∠DAC=60°,PA=AC=2,AB=1. 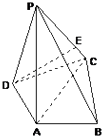
(1)求二面角A﹣PB﹣C的余弦值.
(2)在线段CP上是否存在一点E,使得DE⊥PB,若存在,求线段CE的长度,不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设双曲线C的中心为点O,若有且只有一对相交于点O,所成的角为60°的直线A1B1和A2B2,使| A1B1|=| A2B2|,其中A1,B1和A2,B2分别是这对直线与双曲线C的交点,则该双曲线的离心率的取值范围是( )
A. (![]() ,2] B. [
,2] B. [![]() ,2) C. (
,2) C. (![]() ,+
,+![]() ) D. [
) D. [![]() ,+
,+![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的一个焦点
的一个焦点![]() 与抛物线
与抛物线![]() 的焦点重合,且截抛物线的准线所得弦长为
的焦点重合,且截抛物线的准线所得弦长为![]() .
.
(1)求该椭圆![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
, ![]() 两点,且点
两点,且点![]() 恰为弦
恰为弦![]() 的中点,求直线
的中点,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com