
 ,若不等式a(x2+y2)≥(x+y)2恒成立,则实数a的最小值是
,若不等式a(x2+y2)≥(x+y)2恒成立,则实数a的最小值是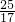


 表示区域内动点P(x,y)与原点连线的斜率,运动点P可得k的取值范围为[2,4].不等式a(x2+y2)≥(x+y)2可化为a≥1+
表示区域内动点P(x,y)与原点连线的斜率,运动点P可得k的取值范围为[2,4].不等式a(x2+y2)≥(x+y)2可化为a≥1+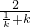 ,再算出不等式右边的最大值,即可得到实数a的最小值.
,再算出不等式右边的最大值,即可得到实数a的最小值. 表示的平面区域,
表示的平面区域,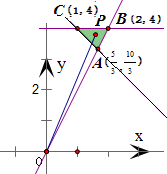
 ,
, ),B(1,4),C(2,4)
),B(1,4),C(2,4) ,表示区域内动点P(x,y)与原点O连线的斜率,
,表示区域内动点P(x,y)与原点O连线的斜率, 的取值范围为[2,4]
的取值范围为[2,4]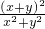 =1+
=1+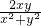 =1+
=1+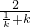
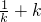 ∈[
∈[ ,
, ]
]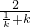 的取值范围为[
的取值范围为[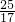 ,
, ]
]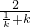 对任意k∈[2,4]恒成立,∴a≥(1+
对任意k∈[2,4]恒成立,∴a≥(1+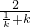 )max=
)max=


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com