
【题目】已知命题p:对于m∈[﹣1,1],不等式a2﹣5a﹣3≥ ![]() 恒成立;命题q:不等式x2+ax+2<0有解,若p∨q为真,且p∧q为假,求a的取值范围.
恒成立;命题q:不等式x2+ax+2<0有解,若p∨q为真,且p∧q为假,求a的取值范围.
【答案】解:若命题p:对于m∈[﹣1,1],不等式a2﹣5a﹣3≥ ![]() 恒成立; 由于
恒成立; 由于 ![]() =3,∴a2﹣5a﹣3≥3,解得a≥6或a≤﹣1.
=3,∴a2﹣5a﹣3≥3,解得a≥6或a≤﹣1.
若命题q:不等式x2+ax+2<0有解,则△=a2﹣8>0,解得 ![]() 或a<﹣2
或a<﹣2 ![]() .
.
若p∨q为真,且p∧q为假,则p与q一真一假.
当p真q假时, 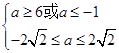 ,解得
,解得 ![]() ,此时a∈
,此时a∈ ![]() .
.
当q真p假时,  ,解得
,解得 ![]() ,此时a∈
,此时a∈ ![]() .
.
综上可知:a的取值范围是 ![]() ∪
∪ ![]()
【解析】分别求出命题p,q中的a的取值范围,再利用若p∨q为真,且p∧q为假,则p与q一真一假.即可得出.
【考点精析】通过灵活运用复合命题的真假,掌握“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真即可以解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】等比数列{an}中,已知a1=2,a4=16.
(1)求数列{an}的通项公式an;
(2)若a3 , a5分别是等差数列{bn}的第4项和第16项,求数列{bn}的通项公式及前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的前n项和为Sn , 若{an}和 ![]() 都是等差数列,且公差相等.
都是等差数列,且公差相等.
(1)求数列{an}的通项公式;
(2)令bn= ![]() ,cn=bnbn+1 , 求数列{cn}的前n项和Tn .
,cn=bnbn+1 , 求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小五、小一、小节、小快、小乐五位同学站成一排,若小一不出现在首位和末位,小五、小节、小乐中有且仅有两人相邻,求能满足条件的不同排法共有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有4个人去参加娱乐活动,该活动有甲、乙两个游戏可供参加者选择.为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏,掷出点数为1或2的人去参加甲游戏,掷出点数大于2的人去参加乙游戏.
(1)求这4个人中恰有2人去参加甲游戏的概率;
(2)求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率;
(3)用X,Y分别表示这4个人中去参加甲、乙游戏的人数,记ξ=|X﹣Y|,求随机变量ξ的分布列与数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个树形图依据下列规律不断生长:1个空心圆点到下一行仅生长出1个实心圆点,1个实心圆点到下一行生长出1个实心圆点和1个空心圆点.则第11行的实心圆点的个数是 . 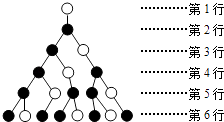
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项都是正数,2a5 , a4 , 4a6成等差数列,且满足 ![]() ,数列{bn}的前n项和为
,数列{bn}的前n项和为 ![]() ,n∈N* , 且b1=1
,n∈N* , 且b1=1
(1)求数列{an},{bn}的通项公式
(2)设 ![]() ,n∈N* , {Cn}前n项和为
,n∈N* , {Cn}前n项和为 ![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com