练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设圆C的圆心与双曲线＝1(a>0)的右焦点重合，且该圆与此双曲线的渐近线相切，若直线l：x－y＝0被圆C截得的弦长等于2，则a的值为________．

     

    【解析】由题知圆心C(，0)，双曲线的渐近线方程为x±ay＝0，圆心C到渐近线的距离d＝＝，即圆C的半径为.由直线l被圆C截得的弦长为2及圆C的半径为可知，圆心C到直线 l的距离为1，即＝1，解得a＝.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学（文）二轮复习真题感悟江苏专用常考问题3练习卷（解析版） 题型：解答题

    如图，在平面直角坐标系xOy中，点A(0,3)，直线l：y＝2x－4.设圆C的半径为1，圆心在l上．

    (1)若圆心C也在直线y＝x－1上，过点A作圆C的切线，求切线的方程；

    (2)若圆C上存在点M，使|MA|＝2|MO|，求圆心C的横坐标a的取值范围．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（文）二轮复习专题提升训练江苏专用阶段检测5练习卷（解析版） 题型：解答题

    如图，正方形ABCD所在的平面与三角形CDE所在的平面交于CD，AE⊥平面CDE，且AB＝2AE.

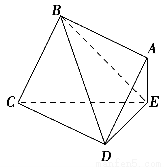
    (1)求证：AB∥平面CDE；

    (2)求证：平面ABCD⊥平面ADE.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（文）二轮复习专题提升训练江苏专用阶段检测4练习卷（解析版） 题型：解答题

    已知直线l：y＝x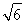＋，圆O：x2＋y2＝5，椭圆E：＝1(a>b>0)的离心率e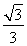＝，直线l被圆O截得的弦长与椭圆的短轴长相等．

    (1)求椭圆E的方程；

    (2)过圆O上任意一点P作椭圆E的两条切线，若切线都存在斜率，求证：两条切线的斜率之积为定值．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（文）二轮复习专题提升训练江苏专用阶段检测4练习卷（解析版） 题型：填空题

    双曲线C：x2－y2＝1，若双曲线C的右顶点为A，过A的直线l与双曲线C的两条渐近线交于P，Q两点，且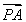＝2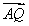，则直线l的斜率为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（文）二轮复习专题提升训练江苏专用阶段检测4练习卷（解析版） 题型：填空题

    圆(x＋2)2＋y2＝4与圆(x－2)2＋(y－1)2＝9的位置关系为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（文）二轮复习专题提升训练江苏专用阶段检测3练习卷（解析版） 题型：解答题

    已知数列{an}和{bn}满足：a1＝λ，an＋1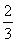＝an＋n－4，bn＝(－1)n(an－3n＋21)，其中λ为实数，n为正整数．

    (1)对任意实数λ，证明：数列{an}不是等比数列；

    (2)试判断数列{bn}是否为等比数列，并证明你的结论．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（文）二轮复习专题提升训练江苏专用阶段检测2练习卷（解析版） 题型：解答题

    在△ABC中，角A，B，C对应的边分别是a，b，c.已知cos 2A－3cos(B＋C)＝1.

    (1)求角A的大小；

    (2)若△ABC的面积S＝5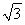，b＝5，求sin Bsin C的值．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（文）二轮复习专题提升训练江苏专用9练习卷（解析版） 题型：填空题

    各项均为正数的等比数列{an}满足a1a7＝4，a6＝8，若函数f(x)＝a1x＋a2x2＋a3x3＋…＋a10x10的导数为f′(x)，则f′＝________.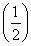

     

    查看答案和解析>>

    同步练习册答案