
ЁОЬтФПЁПФГДГЙигЮЯЗгаетбљвЛИіЛЗНкЃКИУЙиПЈгавЛЕРЩЯСЫЫјЕФУХЃЌвЊЯыЭЈЙ§ИУЙиПЈЃЌвЊФУЕНУХЧАУмТыЯфРяЕФдПГзЃЌВХФмПЊУХЙ§ЙиЃЎЕЋЪЧУмТыЯфашвЊвЛИіУмТыВХФмДђПЊЃЌВЂЧв3ДЮУмТыГЂЪдДэЮѓЃЌИУУмТыЯфБЛЫјЖЈЃЌДгЖјДГЙиЪЇАмЃЎФГШЫЕНДяИУЙиПЈЪБЃЌвбОевЕНСЫПЩФмДђПЊУмТыЯфЕФ6ИіУмТыЃЈЦфжажЛгавЛИіФмДђПЊУмТыЯфЃЉЃЌЫћОіЖЈДгжаЫцЛњЕибЁдё1ИіУмТыНјааГЂЪдЃЎШєУмТые§ШЗЃЌдђЭЈЙиГЩЙІЃЛЗёдђМЬајГЂЪдЃЌжБжСУмТыЯфБЛЫјЖЈЃЎ
ЃЈ1ЃЉЧѓетИіШЫДГЙиЪЇАмЕФИХТЪЃЛ
ЃЈ2ЃЉЩшИУШЫГЂЪдУмТыЕФДЮЪ§ЮЊXЃЌЧѓXЕФЗжВМСаКЭЪ§бЇЦкЭћЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКЩшЁАУмТыЯфБЛЫјЖЈЁБЕФЪТМўЮЊA
дђ ![]()
ЃЈ2ЃЉНтЃКвРЬтвтЃЌXЕФПЩФмШЁжЕЮЊ1ЃЌ2ЃЌ3ЃЌ
дђ ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ\
ЃЌ\
ЫљвдЗжВМСаЮЊЃК
X | 1 | 2 | 3 |
p |
|
|
|
ЫљвдЃК ![]()
ЁОНтЮіЁПЃЈ1ЃЉЩшЁАУмТыЯфБЛЫјЖЈЁБЕФЪТМўЮЊAЃЌРћгУЕШПЩФмЪТМўИХТЪМЦЫуЙЋЪНФмЧѓГіетИіШЫДГЙиЪЇАмЕФИХТЪЃЎЃЈ2ЃЉвРЬтвтЃЌXЕФПЩФмШЁжЕЮЊ1ЃЌ2ЃЌ3ЃЌЗжБ№ЧѓГіЯргІЕФИХТЪЃЌгЩДЫФмЧѓГіXЕФЗжВМСаКЭЪ§бЇЦкЭћЃЎ
ЁОПМЕуОЋЮіЁПНтД№ДЫЬтЕФЙиМќдкгкРэНтРыЩЂаЭЫцЛњБфСПМАЦфЗжВМСаЕФЯрЙижЊЪЖЃЌеЦЮедкЩфЛїЁЂВњЦЗМьбщЕШР§згжаЃЌЖдгкЫцЛњБфСПXПЩФмШЁЕФжЕЃЌЮвУЧПЩвдАДвЛЖЈДЮађвЛвЛСаГіЃЌетбљЕФЫцЛњБфСПНазіРыЩЂаЭЫцЛњБфСПЃЎРыЩЂаЭЫцЛњБфСПЕФЗжВМСаЃКвЛАуЕФ,ЩшРыЩЂаЭЫцЛњБфСПXПЩФмШЁЕФжЕЮЊx1,x2,.....,xi,......,xnЃЌXШЁУПвЛИіжЕ xi(i=1,2,......ЃЉЕФИХТЪP(ІЮ=xiЃЉЃНPiЃЌдђГЦБэЮЊРыЩЂаЭЫцЛњБфСПX ЕФИХТЪЗжВМЃЌМђГЦЗжВМСаЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЧњЯп![]()
ЃЈ1ЃЉШєЧњЯпC1ЪЧвЛИідВЃЌЧвЕуP(1,1)дкдВC1ЭтЃЌЧѓЪЕЪ§mЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЕБm=2ЪБЃЌЧњЯп![]() ЙигкжБЯпx+1=0ЖдГЦЕФЧњЯпЮЊ
ЙигкжБЯпx+1=0ЖдГЦЕФЧњЯпЮЊ![]() ,ЩшPЮЊЦНУцЩЯЕФЕуЃЌТњзуЃКДцдкЙ§PЕуЕФЮоЧюЖрЖдЛЅЯрДЙжБЕФжБЯп
,ЩшPЮЊЦНУцЩЯЕФЕуЃЌТњзуЃКДцдкЙ§PЕуЕФЮоЧюЖрЖдЛЅЯрДЙжБЕФжБЯп![]() ,ЫќУЧЗжБ№гыЧњЯпC1КЭЧњЯп
,ЫќУЧЗжБ№гыЧњЯпC1КЭЧњЯп![]() ЯрНЛЃЌЧвжБЯп
ЯрНЛЃЌЧвжБЯп![]() БЛЧњЯпC1НиЕУЕФЯвГЄгыжБЯпl2БЛЧњЯпC2НиЕУЕФЯвГЄзмЯрЕШ.ЧѓЫљгаТњзуЬѕМўЕФЕуPЕФзјБъЃЛ
БЛЧњЯпC1НиЕУЕФЯвГЄгыжБЯпl2БЛЧњЯпC2НиЕУЕФЯвГЄзмЯрЕШ.ЧѓЫљгаТњзуЬѕМўЕФЕуPЕФзјБъЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкШ§Ртжљ![]() жаЃЌEЃЌFЃЌGЗжБ№ЮЊ
жаЃЌEЃЌFЃЌGЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌABЕФжаЕуЃЎ
ЃЌABЕФжаЕуЃЎ
![]() ЧѓжЄЃКЦНУц
ЧѓжЄЃКЦНУц![]() ЦНУцBEFЃЛ
ЦНУцBEFЃЛ
![]() ШєЦНУц
ШєЦНУц![]() ЃЌЧѓжЄЃКHЮЊBCЕФжаЕуЃЎ
ЃЌЧѓжЄЃКHЮЊBCЕФжаЕуЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪазМБИв§НјгХауЦѓвЕНјааГЧЪаНЈЩш. ГЧЪаЕФМзЕиЁЂввЕиЗжБ№Жд5ИіЦѓвЕЃЈЙВ10ИіЦѓвЕЃЉНјаазлКЯЦРЙРЃЌЕУЗжЧщПіШчОЅвЖЭМЫљЪО.

ЃЈЂёЃЉИљОнОЅвЖЭМЃЌЧѓввЕиЖдЦѓвЕЦРЙРЕУЗжЕФЦНОљжЕКЭЗНВюЃЛ
ЃЈЂђЃЉЙцЖЈЕУЗждк85ЗжвдЩЯЮЊгХауЦѓвЕ. ШєДгМзЁЂввСНЕизМБИв§НјЕФгХауЦѓвЕжаИїЫцЛњбЁШЁ1ИіЃЌЧѓетСНИіЦѓвЕЕУЗжЕФВюЕФОјЖджЕВЛГЌЙ§5ЗжЕФИХТЪ.
зЂЃКЗНВю![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЕиЕчгАдКЮЊСЫСЫНтЕБЕигАУдЖдПьвЊЩЯгГЕФвЛВПЕчгАЕФЦБМлЕФПДЗЈЃЌНјааСЫвЛДЮЕїбаЃЌЕУЕНСЫЦБМлx(ЕЅЮЛЃКдЊ)гыПЪЭћЙлгАШЫЪ§y(ЕЅЮЛЃКЭђШЫ)ЕФНсЙћШчЯТБэЃК
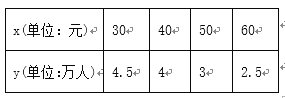
(1)ЧыИљОнЩЯБэЬсЙЉЕФЪ§ОнЃЌгУзюаЁЖўГЫЗЈЧѓГіyЙигкxЕФЯпадЛиЙщЗНГЬЃЛ
(2)ИљОн(1)жаЧѓГіЕФЯпадЛиЙщЗНГЬЃЌШєЦБМлЖЈЮЊ70дЊЃЌдЄВтИУЕчгАдКПЪЭћЙлгАШЫЪ§ЃЎИНЃКЛиЙщжБЯпЕФаБТЪКЭНиОрЕФзюаЁЖўГЫЗЈЙРМЦЙЋЪНЗжБ№ЮЊЃК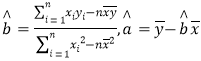
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊдВOЃК![]() ОЙ§Еу
ОЙ§Еу![]() ЃЌгыxжсе§АыжсНЛгкЕуBЃЎ
ЃЌгыxжсе§АыжсНЛгкЕуBЃЎ
![]() Ђё
Ђё![]() ______ЃЛ
______ЃЛ![]() НЋНсЙћжБНгЬюаДдкД№ЬтПЈЕФЯргІЮЛжУЩЯ
НЋНсЙћжБНгЬюаДдкД№ЬтПЈЕФЯргІЮЛжУЩЯ![]()
![]() Ђђ
Ђђ![]() дВOЩЯЪЧЗёДцдкЕуPЃЌЪЙЕУ
дВOЩЯЪЧЗёДцдкЕуPЃЌЪЙЕУ![]() ЕФУцЛ§ЮЊ15ЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЕФУцЛ§ЮЊ15ЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГжжжВдАдкУЂЙћСйНќГЩЪьЪБЃЌЫцЛњДгвЛаЉУЂЙћЪїЩЯеЊЯТ100ИіУЂЙћЃЌЦфжЪСПЗжБ№дк![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЈЕЅЮЛЃКПЫЃЉжаЃЌОЭГМЦЕУЦЕТЪЗжВМжБЗНЭМШчЭМЫљЪО.
ЃЈЕЅЮЛЃКПЫЃЉжаЃЌОЭГМЦЕУЦЕТЪЗжВМжБЗНЭМШчЭМЫљЪО.
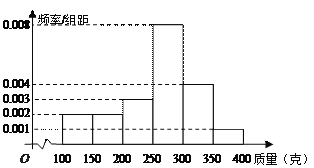
(1) ОМЦЫуЙРМЦетзщЪ§ОнЕФжаЮЛЪ§ЃЛ
(2)ЯжАДЗжВуГщбљДгжЪСПЮЊ![]() ЃЌ
ЃЌ![]() ЕФУЂЙћжаЫцЛњГщШЁ
ЕФУЂЙћжаЫцЛњГщШЁ![]() ИіЃЌдйДгет
ИіЃЌдйДгет![]() ИіжаЫцЛњГщШЁ
ИіжаЫцЛњГщШЁ![]() ИіЃЌЧѓет
ИіЃЌЧѓет![]() ИіУЂЙћжаЧЁга
ИіУЂЙћжаЧЁга![]() Иідк
Иідк![]() ФкЕФИХТЪ.
ФкЕФИХТЪ.
ЃЈ3ЃЉФГОЯњЩЬРДЪеЙКУЂЙћЃЌвдИїзщЪ§ОнЕФжаМфЪ§ДњБэетзщЪ§ОнЕФЦНОљжЕЃЌгУбљБОЙРМЦзмЬхЃЌИУжжжВдАжаЛЙЮДеЊЯТЕФУЂЙћДѓдМЛЙга![]() ИіЃЌОЯњЩЬЬсГіШчЯТСНжжЪеЙКЗНАИЃК
ИіЃЌОЯњЩЬЬсГіШчЯТСНжжЪеЙКЗНАИЃК
AЃКЫљвдУЂЙћвд![]() дЊ/ЧЇПЫЪеЙКЃЛ
дЊ/ЧЇПЫЪеЙКЃЛ
BЃКЖджЪСПЕЭгк![]() ПЫЕФУЂЙћвд
ПЫЕФУЂЙћвд![]() дЊ/ИіЪеЙКЃЌИпгкЛђЕШгк
дЊ/ИіЪеЙКЃЌИпгкЛђЕШгк![]() ПЫЕФвд
ПЫЕФвд![]() дЊ/ИіЪеЙК.
дЊ/ИіЪеЙК.
ЭЈЙ§МЦЫуШЗЖЈжжжВдАбЁдёФФжжЗНАИЛёРћИќЖрЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌФкНЧAЃЌBЃЌCЫљЖдЕФБпЗжБ№ЮЊaЁЂbЁЂcЃЌвбжЊa=csinB+bcosCЃЎ
ЃЈ1ЃЉЧѓA+CЕФжЕЃЛ
ЃЈ2ЃЉШєb= ![]() ЃЌЧѓЁїABCУцЛ§ЕФзюжЕЃЎ
ЃЌЧѓЁїABCУцЛ§ЕФзюжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПКЏЪ§y=ЉsinЃЈІиx+ІеЃЉЃЈІиЃО0ЃЌІеЁЪЃЈЉ ![]() ЃЌ
ЃЌ ![]() ЃЉЃЉЕФвЛЬѕЖдГЦжсЮЊx=
ЃЉЃЉЕФвЛЬѕЖдГЦжсЮЊx= ![]() ЃЌвЛИіЖдГЦжааФЮЊЃЈ
ЃЌвЛИіЖдГЦжааФЮЊЃЈ ![]() ЃЌ0ЃЉЃЌдкЧјМф[0ЃЌ
ЃЌ0ЃЉЃЌдкЧјМф[0ЃЌ ![]() ]ЩЯЕЅЕїЃЎ
]ЩЯЕЅЕїЃЎ
ЃЈ1ЃЉЧѓІиЃЌІеЕФжЕЃЛ
ЃЈ2ЃЉгУУшЕуЗЈзїГіy=sinЃЈІиx+ІеЃЉдк[0ЃЌІа]ЩЯЕФЭМЯѓЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com