精英家教网 > 高中数学 > 题目详情

某同学为了研究学生的性别与是否支持某项活动的关系，运用2×2列联表进行独立性检验，已知样本的观测值K²=7.28，临界值如下表所示：

P（K²≥k₀）	0.1	0.05	0.025	0.01	0.005	0.001
k₀	2.706	3.841	5.024	6.635	7.897	10.828

则有多大把握认为“学生的性别与支持这项活动有关系”（　　）

A、99.9%	B、99.5%
C、99.3%	D、99%

分析：对照临界值表，即可得出结论．

解答：解：∵K²=7.28＞6.635，
对照临界值表：

P（k²≥k₀）	0.100	0.050	0.025	0.010	0.001
k₀	2.706	3.841	5.024	6.635	10.828

∴有99%的把握认为“学生的性别与支持这项活动有关系”．
故选：D．

点评：本题考查独立性检验知识的运用，正确对照临界值表是关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

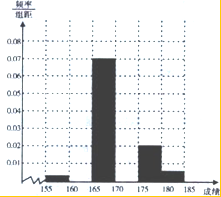某校为了解高三学生的情况，现从期末文综考试成绩中随机抽取100名学生，按成绩分组，得到的频率分布表如图：

组别	分组	频数	频率
1	[155，160]	2	0.020
2	[155，160]	①	0.300
3	[155，160]	35	0.350
4	[155，160]	20	0.200
5	[155，160]	10	②
6	[155，160]	3	0.030
合计		100	1.00

（1）请求出频率分布表中①、②位置相应的数据，并补全频率分布直方图；
（2）若在第4、5组的30人中，用分层抽样抽取6名学生参加体育测试，请问：在第4、5组各抽取多少名学生参加测试？
（3）为了进一步获得研究资料，学校决定在第1组和第6组的学生中，随机抽取3名学生进行心理测试，求第1组中的A同学和第6组中的C同学被同时抽到的概率．

查看答案和解析>>

科目：高中数学 来源： 题型：

有甲乙两个学校进行了一门课程的考试，某同学为了研究成绩与学校是否有关，他进行了如下实验：先将甲校和乙校各300名同学编成1～300号，然后用系统抽样的方法各抽取了20名同学（两校学生抽取号码相同），记录下他们的成绩如下表，表格中部分编号用“×”代替，空缺编号需补充．

编号		18		48		78			123
甲校	75	92	68	92	95	86	75	88	78	45
乙校	92	62	66	77	83	65	77	62	56	82
编号	×	×	×	×	×	×	×	×	×	×
甲校	86	77	85	56	82	77	86	78	88	78
乙校	78	85	66	56	55	91	65	77	79	65

（1）把表格中空白处的编号补充完整．
（2）若规定该课程分数在80分以上为“优秀”，80分以下为“非优秀”
（Ⅰ）从乙校成绩为“优秀”的学生中随机抽取2人，求两人的分数都不高于90分的概率．
（Ⅱ）试分析有多大把握认为“成绩与学校有关系”．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

有甲乙两个学校进行了一门课程的考试，某同学为了研究成绩与学校是否有关，他进行了如下实验：先将甲校和乙校各300名同学编成1～300号，然后用系统抽样的方法各抽取了20名同学（两校学生抽取号码相同），记录下他们的成绩如下表，表格中部分编号用“×”代替，空缺编号需补充．
编号 18 48 78 123
甲校 75 92 68 92 95 86 75 88 78 45
乙校 92 62 66 77 83 65 77 62 56 82
编号 × × × × × × × × × ×
甲校 86 77 85 56 82 77 86 78 88 78
乙校 78 85 66 56 55 91 65 77 79 65
（1）把表格中空白处的编号补充完整．
（2）若规定该课程分数在80分以上为“优秀”，80分以下为“非优秀”
（Ⅰ）从乙校成绩为“优秀”的学生中随机抽取2人，求两人的分数都不高于90分的概率．
（Ⅱ）试分析有多大把握认为“成绩与学校有关系”．

查看答案和解析>>

科目：高中数学 来源：2010年广东省佛山市南海区高考题例研究数学试卷（文科）（解析版） 题型：解答题

编号		18		48		78			123
甲校	75	92	68	92	95	86	75	88	78	45
乙校	92	62	66	77	83	65	77	62	56	82
编号	×	×	×	×	×	×	×	×	×	×
甲校	86	77	85	56	82	77	86	78	88	78
乙校	78	85	66	56	55	91	65	77	79	65

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学