
已知R上的不间断函数 满足:①当
满足:①当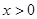 时,
时, 恒成立;②对任意的
恒成立;②对任意的 都有
都有 。又函数
。又函数 满足:对任意的
满足:对任意的 ,都有
,都有 成立,当
成立,当 时,
时, 。若关于
。若关于 的不等式
的不等式 对
对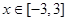 恒成立,则
恒成立,则 的取值范围( )
的取值范围( )
A.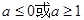 | B. | C.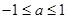 | D.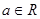 |
A
解析试题分析:因为,当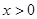 时,
时, 恒成立,所以,函数
恒成立,所以,函数 在区间(0,+∞)是增函数;又对任意的
在区间(0,+∞)是增函数;又对任意的 都有
都有 。所以,
。所以, 是偶函数,且有g|(x|)=g(x)。而函数
是偶函数,且有g|(x|)=g(x)。而函数 满足:对任意的
满足:对任意的 ,都有
,都有 成立,所有函数
成立,所有函数 是周期函数,周期为
是周期函数,周期为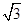 。所以g[f(x)]≤g(a2-a+2)在R上恒成立,
。所以g[f(x)]≤g(a2-a+2)在R上恒成立,
∴|f(x)|≤|a2-a+2|对x∈[-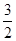 -2
-2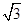 ,
,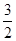 -2
-2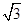 ]恒成立,
]恒成立,
只要使得定义域内|f(x)|max≤|a2-a+2|min,
由于当x∈[-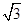 ,
,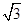 ]时,f(x)=x3-3x,
]时,f(x)=x3-3x,
所以,f′(x)=3x2-3=3(x+1)(x-1),
该函数过点(-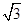 ,0),(0,0),(
,0),(0,0),(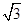 ,0),
,0),
且函数在x=-1处取得极大值f(-1)=2,
在x=1处取得极小值f(1)=-2,
又函数 是周期函数,周期为
是周期函数,周期为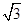
所以函数f(x)在x∈[-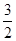 -2
-2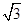 ,
,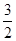 -2
-2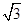 ]的最大值为2,所以,令2≤|a2-a+2|解得:a≥1或a≤0.
]的最大值为2,所以,令2≤|a2-a+2|解得:a≥1或a≤0.
选A.考点:利用导数研究函数的单调性、最值,函数的奇偶性、周期性,函数不等式。
点评:中档题,解函数不等式,往往需要将不等式具体化或利用函数的图象,结合函数的单调性。总之,要通过充分认识函数的特征,探寻解题的途径。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:单选题
求形如 的函数的导数,我们常采用以下做法:先两边同取自然对数得:
的函数的导数,我们常采用以下做法:先两边同取自然对数得: ,再两边同时求导得
,再两边同时求导得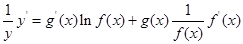 ,于是得到:
,于是得到: ,运用此方法求得函数
,运用此方法求得函数 的一个单调递增区间是( )
的一个单调递增区间是( )
A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知函数 的定义域为
的定义域为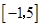 ,部分对应值如下表.
,部分对应值如下表.
 的导函数
的导函数 的图象如图所示.
的图象如图所示.
下列关于函数 的命题:①函数
的命题:①函数 在
在 是减函数;
是减函数;
②如果当 时,
时, 的最大值是2,那么
的最大值是2,那么 的最大值为4;
的最大值为4;
③当 时,函数
时,函数 有4个零点.
有4个零点.
其中真命题的个数是
| A.0个 | B.3个 | C. 2个 | D.1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com